概率论与数理统计知识点

第一章概率论基础

1.1 随机事件与样本空间

随机试验：可重复进行，结果预先知道

样本空间：随机试验的一切可能结果组成的集合，称为样本空间

1.2 事件之间的关系与运算

关系：包含、并交、互不相容（互斥）、差、对立

运算：交换律、结合律、分配率、摩根定律

1.3 随机事件的概率

统计概率、古典概率、几何概率，略

1.4 条件概率全概率公式与贝叶斯公式

P(B|A)=P(AB)/P(A)，指的是在A发生的情况下B发生的概率

全概率公式

$P(A)=\sum_{i=1}^nP(A|Bi)P(Bi)$

贝叶斯公式（逆概率公式）

$P(Bi|A)=\frac {P(BiA)}{P(A)}= \frac {P(A|Bi)P(Bi)}{\sum_{j=1}^nP(A|Bj)P(Bj)} \ ,\ i=1,2,...,n$

实际上，贝叶斯公式可以不用记住，由条件概率和全概率公式推导即可

1.5 事件的独立性

定义：对两个事件A、B，如果P(AB)=P(A)P(B)，则称A、B相互独立

定理：①设A、B是相互独立的事件，若P(A)>0，则P(B|A)=P(B)；若P(B)>0，则P(A|B)=P(A)

②设A、B是相互独立的事件，则下列各对事件也相互独立：A与B非、A非与B、A非与B非

1.6 常用公式总结

减法公式：P(A-B)=P(A)-P(AB)

两个事件的并：P(A∪B)=P(A)+P(B)-P(AB)

三个事件的并：P(A∪B∪C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)

第二章随机变量及其分布

2.1 随机变量的概念

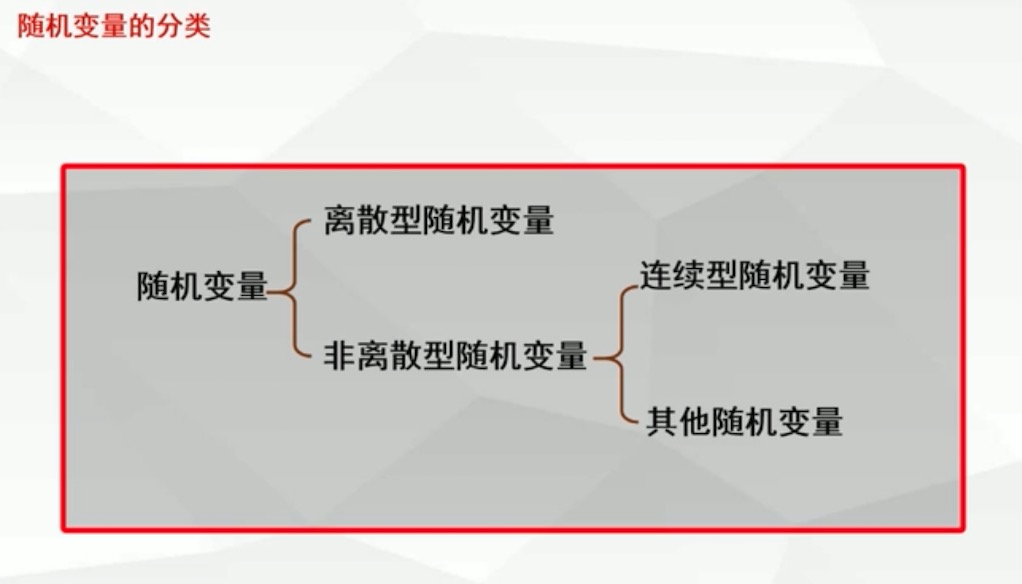
随机试验结果两类表示方法

1.数量化表示

如：网课注册人数，Ω={0,1,2,3,…}

2.非数量化表示

如：抛硬币，观察证明H和反面T出现的情况，Ω={H,T}

随机变量函数

设E是随机试验，它的样本空间为Ω={w}，对于每一个w∈Ω，都有一个实数X(w)与之对应，得到一个定义在Ω上的单值实值函数X(w)，称X(w)为随机变量函数，简称随机变量。

离散型随机变量：

2.2 离散型随机变量及其概率分布率

2.2.1 两点分布和二项分布

两点分布：对于一次随机试验，事件A与A非有且只有一个发生，P(A)=p，则P(A非)=1-p，这样的实验称为 伯努利试验 ，如上班是否迟到，考试是否及格

二项分布：

2.2.2 泊松分布、几何分布、超几何分布

泊松分布

设随机变量的可能取值为0,1,2,…，取各个值的概率为：

$P\{X=k\}=\frac{\lambda^ke^{-\lambda}}{k!}\ ,\ k=0,1,2,...$

其中λ>0是常数，则称X服从参数为λ的泊松分布，记为X~P(λ)

几何分布

在伯努利试验中，若每次试验中事件A发生的概率为p，X表示实验中A首次发生的试验次数，X的取值为1,2,… ，则称X服从参数p的 几何分布

$P\{X=K\}=(1-p)^{k-1}p$

其中，k=1,2,3,… 记作X~G (p)

其常用来描述 事件首次成功 的概率模型

超几何分布

设N件产品中有M件次品，从中任取n件产品，得到的次品数X为随机变量

$P\{X=k\}\frac{C{^k_M}C{^{n-k}_{N-M}}}{C{^n_N}},k=0,1,2,...,min\{n,M\}$

则称X服从超几何分布

注意：有放回抽样->二项分布无放回抽样->超几何分布

2.3 随机变量的分布函数

定义：设X是一个随机变量，x为任意实数，函数F(x) = P{X ≤ x}称为X的概率分布函数，简称分布函数

由性质判定分布函数：

性质1：0≤F(x)≤1，x∈(-∞,+∞)

性质2：F(x1)≤F(x2)，(x1<x2) 单调不减

性质3：lim(x->x0+)F(x) = F(x0), (-∞ < x0 <+∞) 右连续

2.4 连续型随机变量

2.4.1 连续型随机变量概念

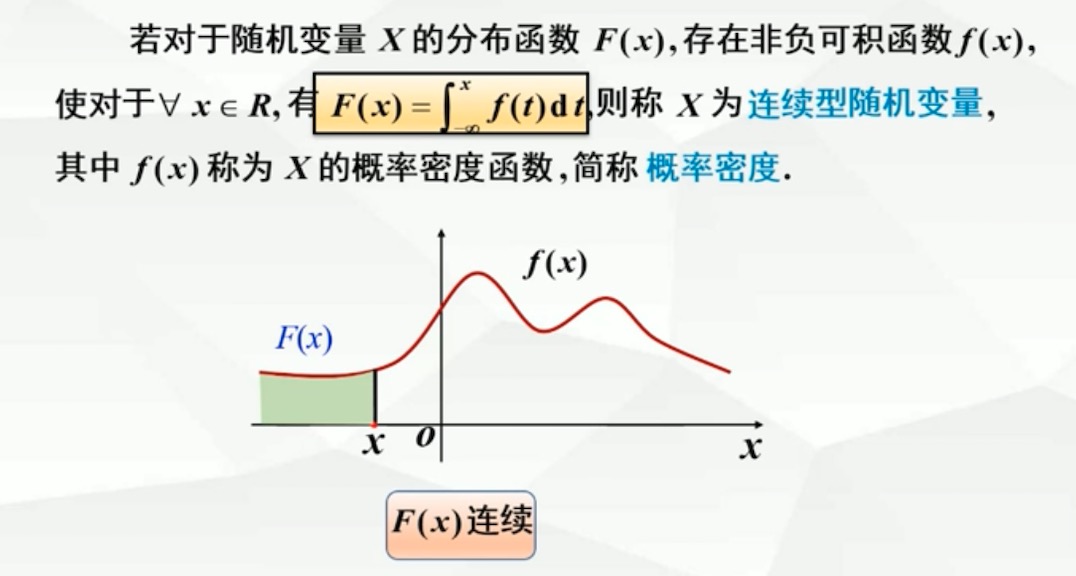
性质：

1.f(x) ≥ 0

$\int^{+∞}_{-∞}f(x)dx = 1$

满足以上两个条件的函数，可作为随机变量的概率密度函数

$P\{x_1 < X ≤ x_2\} = F(x_2)-F(x_1)=\int^{x_2}_{x_1}f(x)dx$

注意：对于任意可能值a，连续型随机变量取a的概率为0（落入某一区间概率与开闭无关）

4.若f(x)在点x处连续，则有F’(x) = f(x)

2.4.2 均匀分布与指数分布

均匀分布

指数分布

指数分布是独立事件发生的时间间隔的分布
指数分布具有无记忆性

2.4.3 正态分布

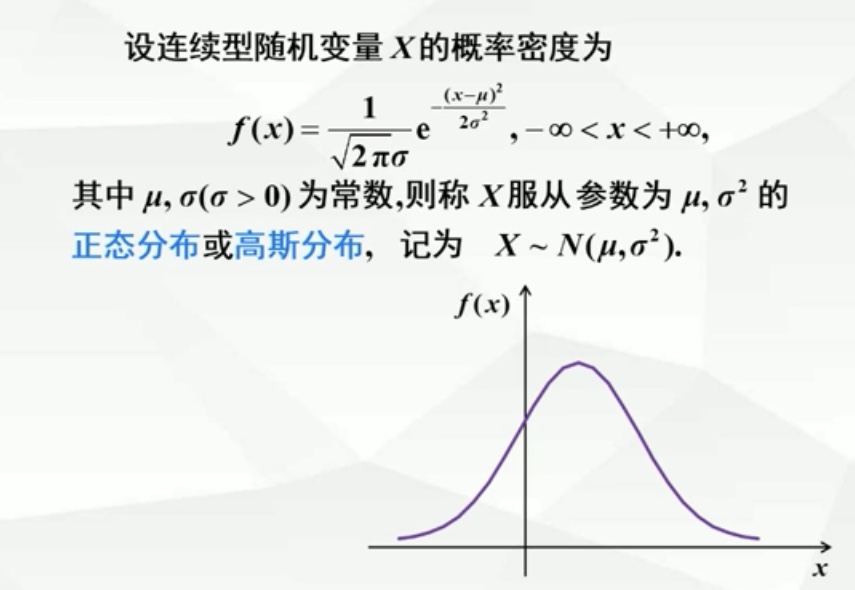
p8-正态分布

标准正态分布

当正态分布N(μ, σ²)中的μ=0，σ=1时，这样的分布称为标准正态分布
几何特征

当σ不变，改变μ大小，相当于f(x)平移变换，反之则对称轴不变，图形高度随σ越大越低
性质
- 1.Φ(-x) = 1 - Φ(x)
- 2.若X~N(μ, σ²)，则Z=(X-μ)/σ ~ N(0, 1) （标准化）
标准化例题

2.5 一维随机变量的函数分布

若X是离散型随机变量，则Y=g(x)也一定是离散型随机变量

公式法求概率密度

第三章多维随机变量及其分布

3.1 二维随机变量

3.1.1 二维随机变量及其分布函数

定义：E是一个随机试验，它的样本空间为Ω={w}，设X=X(w)和Y=Y(w)是定义在Ω上的随机变量，由他们构成的一个向量(X,Y)，叫作二维随机向量或二维随机变量。
分布函数

设(X,Y)是二维随机变量，对于任意实数x,y，二元函数：F(x,y)=P{(X≤x)∩(Y≤y)} = P{X≤x, Y≤y}

上面函数称为二维随机变量(X,Y)的分布函数，或称为随机变量X和Y的联合分布函数
分布函数性质
- 1）对一切x,y，有0≤F(x,y)≤1
- 2）F(x,y)分别对x,y是单调不减的函数
- 3）对于固定的x, F(x,-∞) = lim(y->-∞)F(x,y)=0 F(-∞,y)=lim(x->-∞)F(x,y)=0
- 4）F(x,y)分别是x和y的右连续函数
- 5）对于任意的x1<x2, y1<y2都有：F(x2,y2) - F(x1,y2) - F(x2,y1) + F(x1,y1) ≥ 0

3.1.2 二维离散型随机变量

若二维随机变量(X,Y)所取的可能值是有限对或无限可列多对，则称(X,Y)为二维离散型随机变量
二维随机变量(X,Y)的分布律 - 又称为随机变量X,Y的联合分布律，所有概率和为1

3.1.3 二维连续型随机变量

对于(X, Y)的分布函数F(x,y)，如果存在非负的函数f(x,y)使对任意实数x,y都有

$F(x,y) = \int^{y}_{-∞}\int^{x}_{-∞}f(u,v) dudv$

则称(X,Y)是连续型的二维随机变量，函数f(x,y)称为二维随机变量(X,Y)的概率密度，或称为随机变量X,Y的联合概率密度
概率密度函数性质
- 1. f(x,y)≥0
- $\int^{+∞}_{-∞}\int^{+∞}_{-∞}f(x,y) dxdy=1$
  1. 设G是xoy平面上的一个区域，则 P{ {X,Y} ∈ G } = 对f(x,y)中G区域的积分
- 1. 若f(x,y)在点(x,y)连续，则有f(x,y) = a²F(x,y) / axay = f(x,y)

3.1.4 二维常用分布 n维随机变量概念

均匀分布

定义：设D是平面上的有界区域，其面积为S，若(X,Y)具有概率密度f(x,y)=1/S , (x,y)∈D 或 0, 其他

则称(X,Y)在D上服从均匀分布
二维正态分布
n维随机变量

定义：设E是一个随机试验，它的样本空间是Ω={w}，设X1=X1(w)，X2=X2(w)，…，Xn=Xn(w)，是定义在Ω上的随机变量，由它们构成的一个n维向量(X1,X2,…,Xn)叫做n维随机向量或n维随机变量。

3.2 边缘分布

3.2.1 边缘分布函数、边缘分布律

二维随机变量(X,Y)作为整体，具有联合分布函数F(x,y)，而X和Y自己也有分布函数，分别记为Fx(x),Fy(y)

即分别称为X和Y的边缘分布函数。同时还有边缘概率密度和边缘分布率的概念，将它们统称为边缘分布。
求边缘分布函数示例
离散型随机变量分布律（求法）

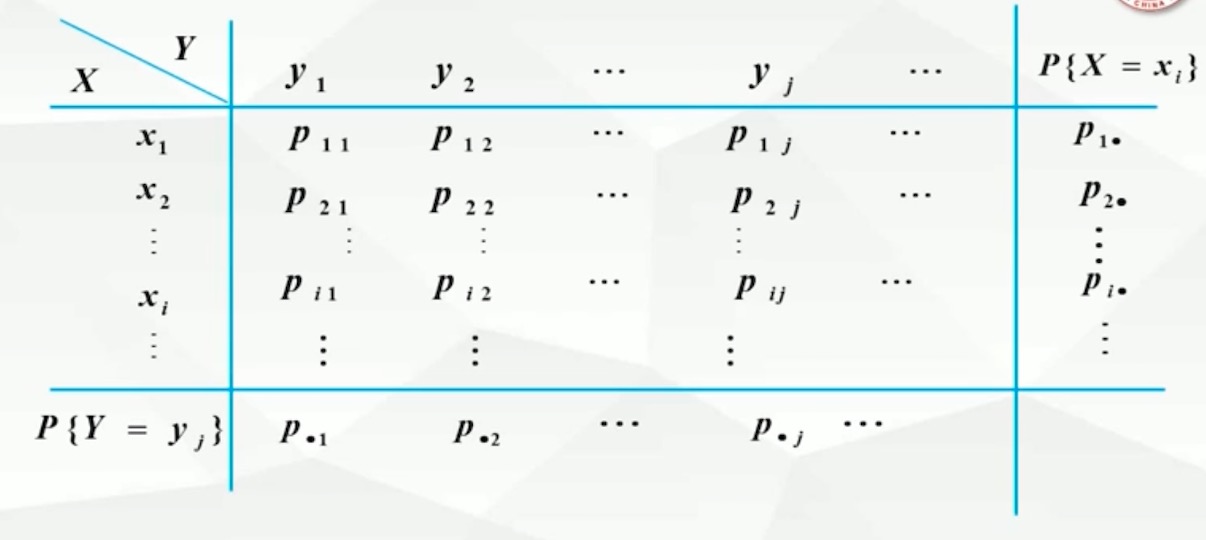
3.2.2 连续型随机变量的边缘分布

随机变量的独立性概念

由两事件独立的定义是P(AB)=P(A)P(B)，推广得到：

设F(x,y)及Fx(X)，Fy(y)分别是二维随机变量(X,Y)的分布函数及边缘分布函数，若对于任意实数x,y有P{X≤x, Y≤y} = P{X≤x}P{Y≤y}，即F(x,y)=Fx(x)Fy(y)，则称随机变量X和Y是相互独立的

（重要结论：随机变量X和Y相互独立的话，g1(X)与g2(X)也相互独立，其中g为一元连续函数）
对于连续型随机变量(X,Y)，设它的概率密度为f(x,y)

$则有：f_X(x)=F_X'(x)=\int^{+∞}_{-∞}f(x,y) dy \\ f_Y(y)=F_Y'(y)=\int^{+∞}_{-∞}f(x,y) dx$

上面称为随机变量(X,Y)分别关于X，Y的边缘概率密度
二维正态分布的边缘概率密度

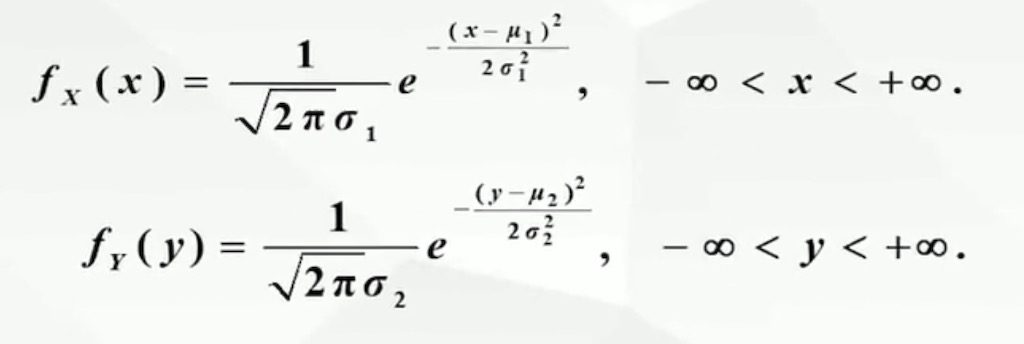
注意：边缘分布为正态分布的随机变量，联合分布不一定是二维正态分布

3.3 随机变量的独立性

离散型随机变量的独立性

离散型随机变量X和Y相互独立的充分必要条件：P{X=xi, Y=yj}=P{X=xi}P(Y=yj)
连续型随机变量的独立性

连续型随机变量X和Y相互独立的充分必要条件：f(x,y)=fx(x)*fy(y)，几乎处处成立（除去平面上面积为0的集合）
二维正态变量的两个分量相互独立的充要条件：N(μ1,μ2,σ1²,σ2²,ρ)中的参数ρ=0
多维随机变量独立性及性质

3.4 条件分布

定义：设(X,Y)是二维离散型随机变量，对于固定的j若P(Y = yj)>0, 则称

$P(X=x_i|Y=y_j)=\frac{P(X=x_i,Y=y_j)}{P(Y=y_j)}=\frac{P_{ij}}{P_{*j}}$

为在Y=yj条件下随机变量X的条件分布律

对于固定的i，若P(X=xi)>0，则称

$P(Y=y_j|X=x_i)=\frac{P(X=x_i,Y=y_j)}{P(X=x_i)}=\frac{P_{ij}}{P_{i*}}$

为在X=xi条件下随机变量Y的条件分布律

二维连续型随机变量的条件分布

设二维连续型随机变量(X,Y)概率密度为f(x,y)，关于Y的边缘概率密度为fY(y)，若对固定的y，fY(y)>0则称

$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$

为在Y=y条件下随机变量X的条件概率密度

相反地，关于Y的边缘概率密度为fX(x)，若对固定的x，fX(x)>0则称

$f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)}$

为在X=x条件下随机变量Y的条件概率密度
联合分布、边缘分布、条件分布关系如下

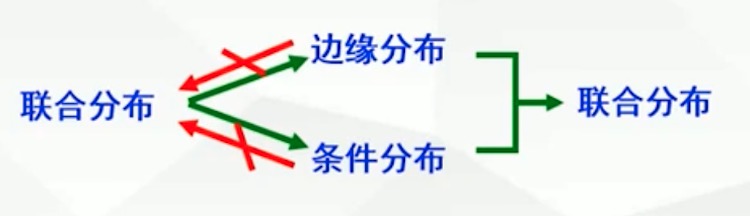
3.5 二维随机变量的函数的分布

3.5.1 二维随机变量的函数分布与概率密度

函数分布

把二维随机变量分布律表写成坐标形式，并省略掉联合分布律为0的点，随后将(X,Y)的值代入函数X-Y得对应的函数值
概率密度

二维连续型随机变量函数的概率密度

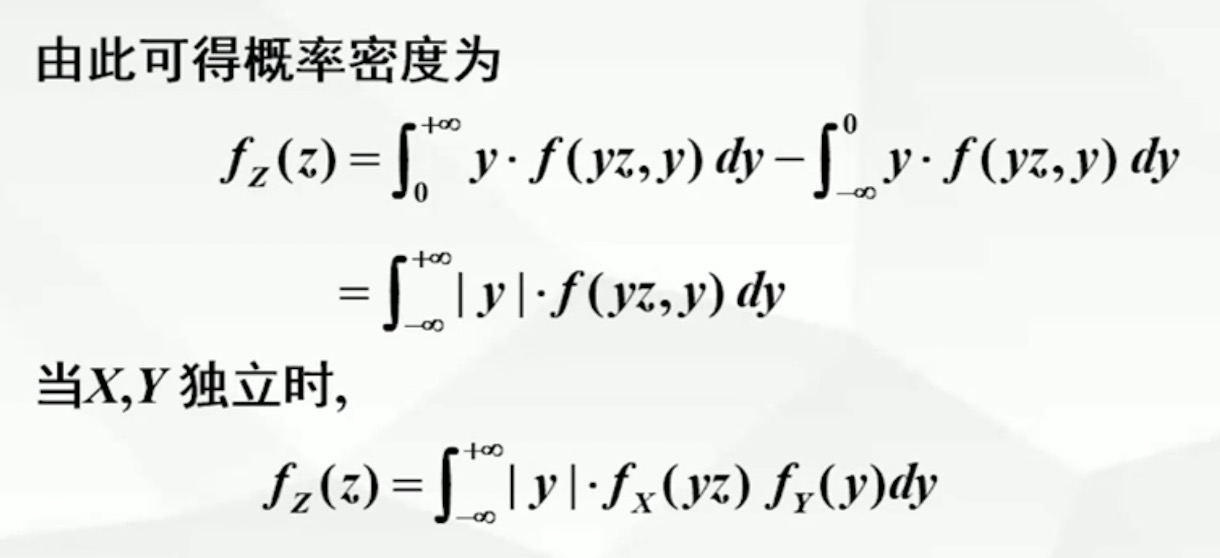
3.5.2 Z=X+Y的分布

Z=X+Y的概率密度计算公式
结论：独立的正态分布的和仍是正态分布

3.5.3 max(X,Y)与min(X,Y)的分布

设X, Y是两个相互独立的随机变量，他们的分布函数分别为FX(x)和FY(y)，另M=max(X,Y)，N=min(X,Y)，则
$F_{max}(z)=F_X(z)F_Y(z)\\ F_{min}(z)=1-(1-F_X(z))(1-F_Y(z))$

推导过程

$F_{max}(z)=P(M≤z)=P(X≤z,Y≤z)=P(X≤z)P(Y≤z)=F_X(z)F_Y(z)\\ F_{min}(z)=P(N≤z)=1-P(N＞z)=1-P(X＞z,Y＞z)=1-P(X＞z)P(Y＞z) =1-(1-F_X(z))(1-F_Y(z))$

第四章随机变量的数字特征

4.1 随机变量的数学期望

数学期望的本质：以概率为权重对随机变量取值加权平均

4.1.1 离散型随机变量的数学期望

定义

4.1.2 连续型随机变量的数学期望

定义

4.1.3 随机变量函数的数学期望

一维随机变量函数的数学期望

(1)若X是离散型随机变量，分布列为P{X=xi}=pi，则E(Y)=E[g(X)]=∑g(xi)pi

(2)若X是连续型随机变量，密度函数为f(x)，则E(Y)=E[g(X)]=∫(-∞,+∞)g(x)f(x)dx
二维随机变量函数的数学期望

由一维随机变量数学期望推广可得

4.1.4 数学期望的性质

性质如下

(1)设C是常数，则有E(C)=C

(2)设X是一个随机变量，C是常数，则有E(CX)=CE(X)

(3)设X，Y是两个随机变量，则有E(X+Y)=E(X)+E(Y)

(4)设X，Y是相互独立的随机变量，E(XY)=E(X)E(Y)

4.2 随机变量的方差与标准差

4.2.1 方差与标准差的定义

方差的定义

设X是一个随机变量，若E{[X-E(X)]²}存在，则称E{[X-E(X)]²}为X的方差，记为D(X)或Var(X)，称根号D(X)为标准差或均方差。

注意：方差的本质是随机变量与数学期望之间的平均偏离程度

计算公式：D(X)=E(X²)-E(X)²

4.2.2 方差的性质

性质如下

(1) 设C是常数，则D(C)=0

(2) 设C是常数，X是随机变量，则D(CX)=C²D(X)

(3) 设X,Y独立，D(X)，D(Y)存在，则D(X±Y)=D(X)+D(Y)

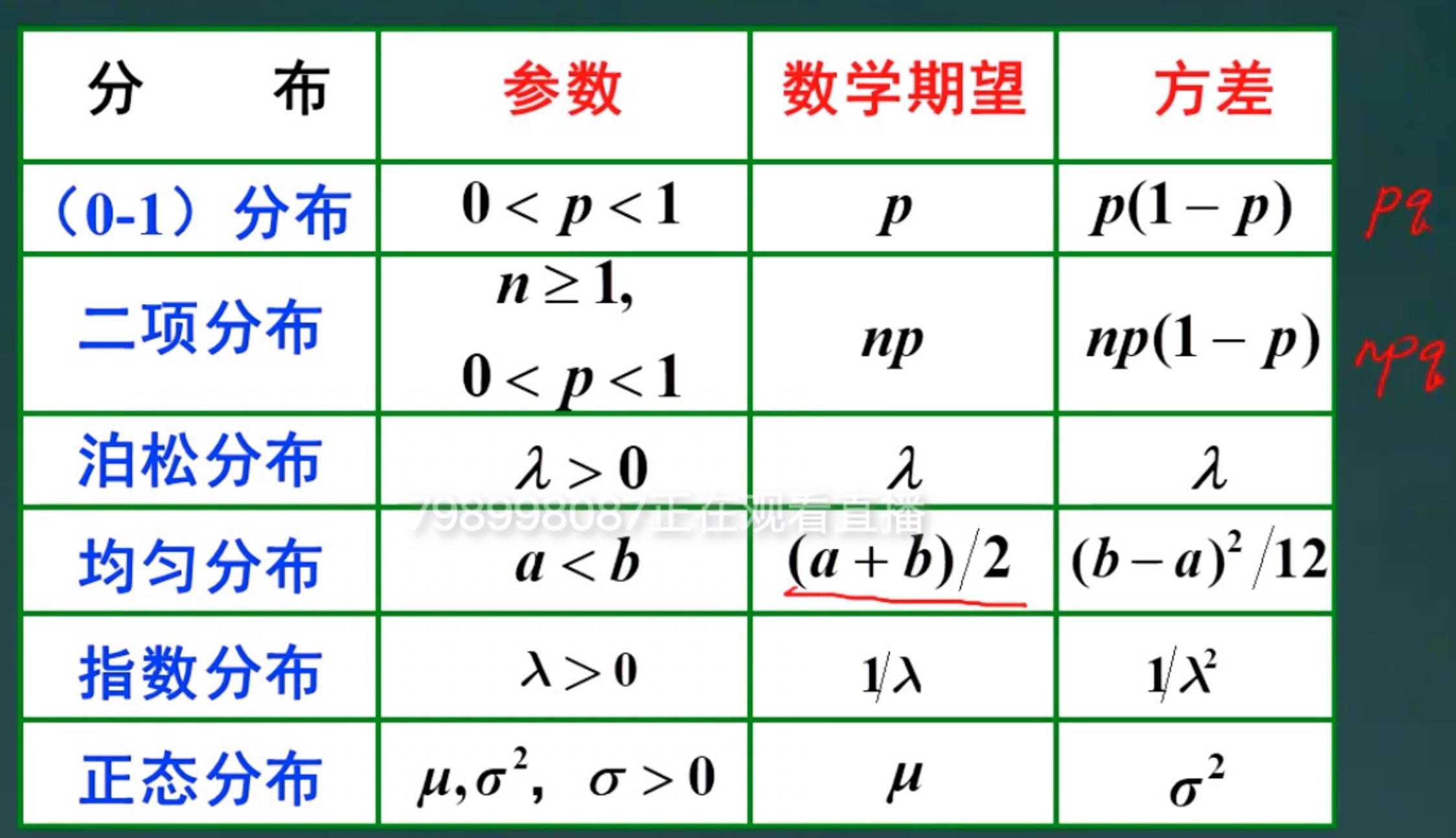
4.3 几种常见分布的数学期望和方差

总结如下
例题：设X~B(n,p)，且E(X)=2.4，D(X)=1.44，求n和p

解：由E(X)=np=2.4，D(X)=npq=1.44，故q=0.6, p=0.4, n=6

4.4 协方差

定义

E{[X-E(X)][Y-E(Y)]}称为随机变量X与Y的协方差，记为Cov(X,Y)
计算公式

(1) Cov(X,Y) = E(XY) - E(X)E(Y)

(2) Cov(X,X) = D(X)
性质

(1) Cov(X,Y) = Cov(Y,X) 对称性

(2) Cov(aX,bY) = abCov(X,Y) a,b为常数

(3) Cov(X1+X2, Y) = Cov(X1,Y) + Cov(X2,Y)

(4) 若X,Y独立，那么Cov(X,Y) = 0 （倒推不成立）

(5) D(X±Y) = D(X)+D(Y)±2Cov(X,Y)

4.5 相关系数

矩

若 E(X^k) (k=1,2,…) 存在，则称它为X的k阶原点矩
若 E[X-E(X)]^k (k=1,2,…) 存在，则称它为X的k阶中心矩

注意：数学期望、方差、协方差都是特殊的矩

第五章大数定律与中心极限定律

5.1 切比雪夫不等式与大数定律

5.1.1 依概率收敛、切比雪夫不等式

依概率收敛

定义：设Y1,Y2,…,Yn是一随机变量序列，a是一个常数，若对于任意整数ε，有lim(n->+∞)P{|Yn - a|≥ε} = 0，则称序列Y1,Y2,…,Yn依概率收敛于a，记为Yn—>a，当n->+∞
性质

设Xn—>a, Yn—>b, 当n->+∞，设函数g(x,y)在点(a,b)连续，则g(Xn,Yn)—>g(a,b)，当n->+∞

切比雪夫不等式

定理：对任意随机变量X，设E(X)，D(X)都存在，则∀ε>0，P{|X-E(X)|≥ε} ≤ D(X)/ε²，等价形式：P{|X-E(X)|＜ε}≥1-D(X)/ε²
优点：不需知道X的分布，适用范围广
缺点：估计较粗糙

5.1.2 伯努利大数定律

定理

设na是n次重复独立实验中事件A发生的次数，p=p(A)，则∀ε>0，有

$\lim\limits_{n \rightarrow \infty} P\{|\frac{n_A}{n}-p|≥ε\}=0$

注意：“伯努利大数定律”是频率稳定性的准确描述

5.1.3 切比雪夫大数定律、辛钦大数定律

切比雪夫大数定律-定理

设相互独立的随机变量序列X1, X2, … , Xn,… 期望与方差都存在，且方差是一致有上界的，即存在正常数C，使得D(Xk)≤C，k=1,2,…，则对于任意整数ε，有

$\lim\limits_{n \rightarrow \infty} P\{|\frac1n\sum_{k=1}^nX_k-E(\frac1n\sum_{k=1}^nX_k)|≥ε\}=0$
辛钦大数定律-定理

设独立同分布的随机变量序列X1,X2,…,Xn,…，期望存在，记为μ，则对任意整数ε，有

$\lim\limits_{n \rightarrow \infty} P\{|\frac1n\sum_{k=1}^nX_k-μ|≥ε\}=0$

5.2 中心极限定理

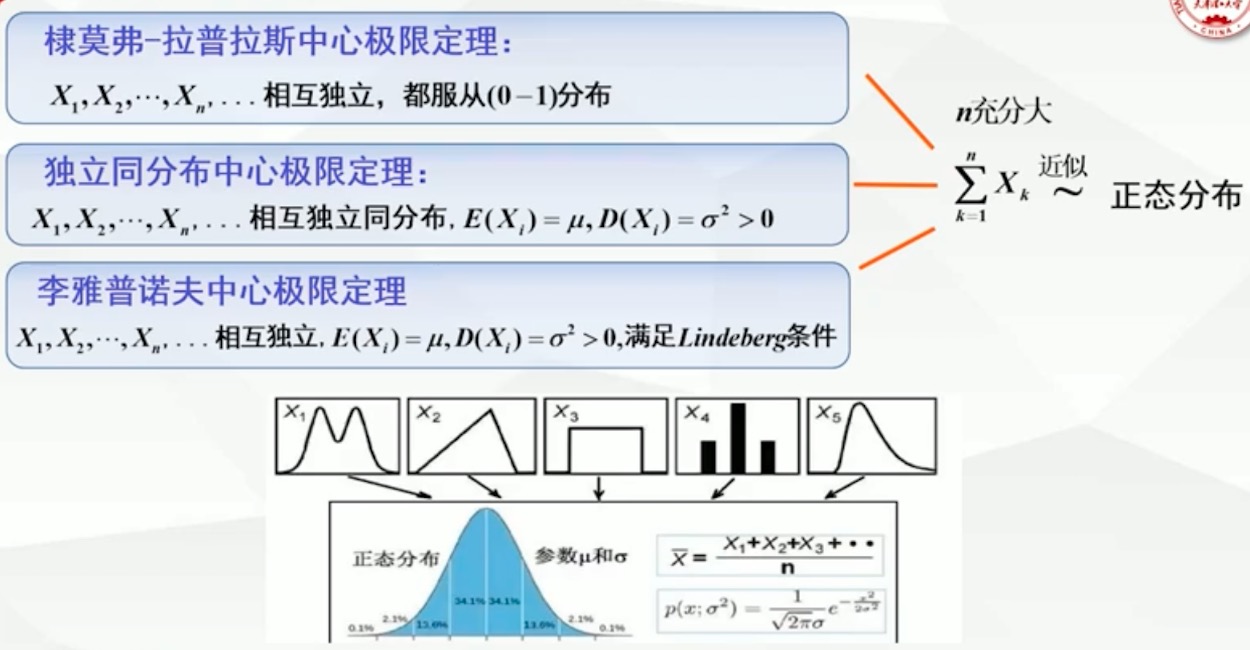
5.2.1 埭莫弗-拉普拉斯中心极限定理

定理

设随机变量Yn~B(n,p)(n=1,2,…; 0<p<1, q=1-p)，Zn=(Yn-np) / 根号npq

则对任意实数x，恒有lim(n->∞)Fzn(x)=Φ(x)
说明

当n充分大时，Zn近似服从N(0,1)，Yn近似服从N(np, npq)

5.2.2 独立同分布中心极限定理

定理

各种中心极限定理的比较

如下图所示

第六章数理统计的基本概念

6.1 总体与样本

总体

研究对象的某项数量指标值的全体
个体

构成总体的每个元素

注意：用大写X1 X2 … 表示样本，小写x1 x2… 表示样本值
样本

简单随机抽样，要求抽取的样本满足：

1）样本具有代表性，即Xi与总体X同分布

2）样本具有独立性：X1,X2,…,Xn相互独立

用上述抽样方法得到的样本称为简单随机样本，简称样本

6.2 统计量

概念

不含有任何未知参数的样本函数
定义

设X1,X2,…,Xn是来自总体X的一个样本，若样本函数g(X1,X2,…,Xn)中不含有任何未知参数，则称g(X1,X2,…,Xn)是一个统计量
常用统计量

设X1,X2,…,Xn是来自总体X的一个样本，x1,x2,…,xn是这样本的观测值

1）样本平均值

$\overline X=\frac1n\sum_{i=1}^nX_i$

2）样本方差

$S^2=\frac1{n-1}\sum_{i=1}^n(X_i-\overline X)^2$

3）样本标准差

$S=\sqrt {S^2}$

4）样本矩——样本k阶（原点）矩（k=1,2…）

$A_k=\frac1n\sum_{i=1}^n{X_i}^k$

注意：样本1阶矩即为样本平均值
5）样本矩——样本k阶中心矩（k=2,3,…)

$B_k=\frac1n\sum_{i=1}^n(X_i-\overline X)^k$
常用统计量常用结论

1）样本方差常用变形公式

$S^2=\frac1{n-1}(\sum_{i=1}^n{X_i}^2-n{\overline X}^2)$

2）对任意总体X，设E(X)=μ，D(X)=σ²，X1,X2,…,Xn是样本，则E(X平均)=μ，D(X平均)=σ²/n，E(S²)=σ²

6.3 抽样分布

统计量的分布称为抽样分布

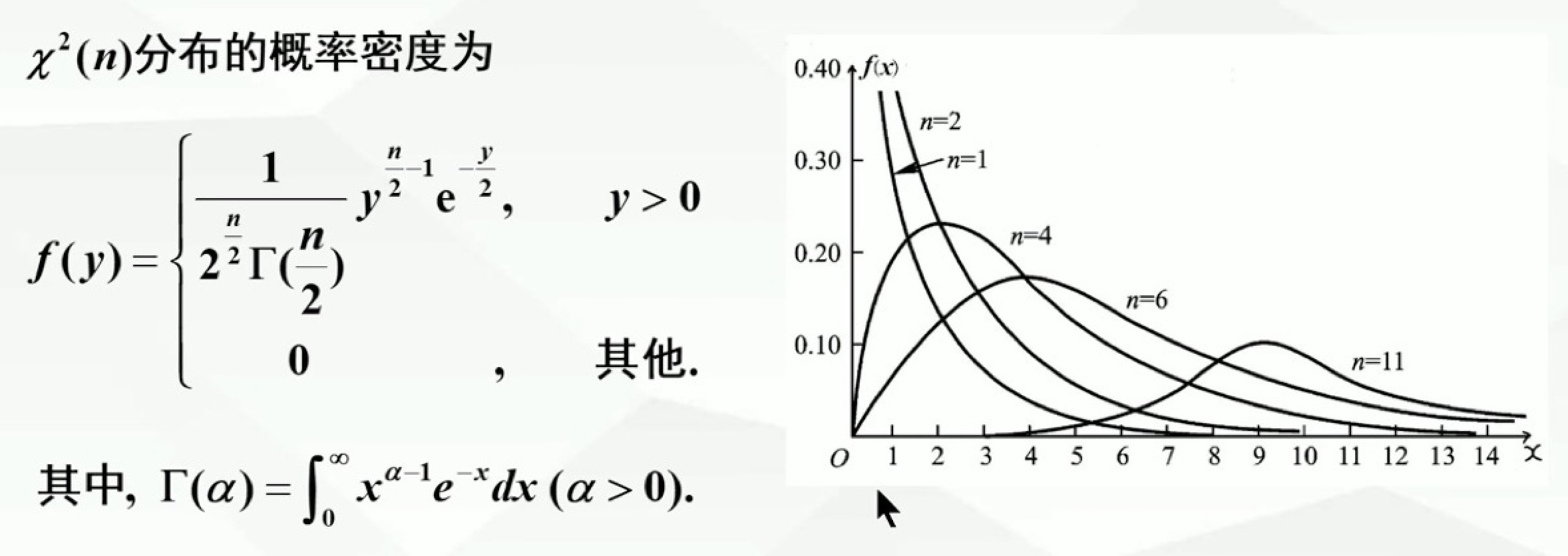
6.3.1 X²分布

设随机变量X1,X2,…,Xn相互独立，且都服从N(0,1)，则称统计量X²=X1²+X2²+…+Xn²服从自由度为n的X²分布，记为X²~X²(n)
自由度：指X²=X1²+X2²+…+Xn²中右端包含独立变量的个数
性质

1）X²分布的可加性

设X1²~X²(n1)，X2²~X²(n2)，并且X1²与X2²相互独立，则X1²+X2²~X²(n1+n2)

2）X²分布随机变量的数学期望和方差

若X²~X²(n)，则E(X²)=n，D(X²)=2n
例题

注意：这里用到了正态分布标准化，如下所示：

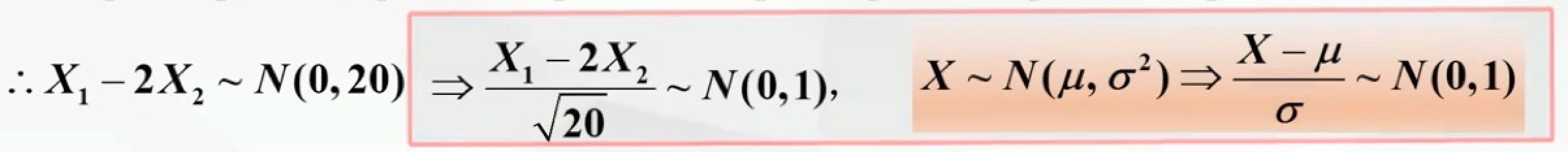
6.3.2 t分布、F分布

t分布

设X~N(0,1)，Y~X²(n)，且X与Y相互独立，则称随机变量t=X/根号(Y/n)服从自由度为n的t分布，记为t~t(n)

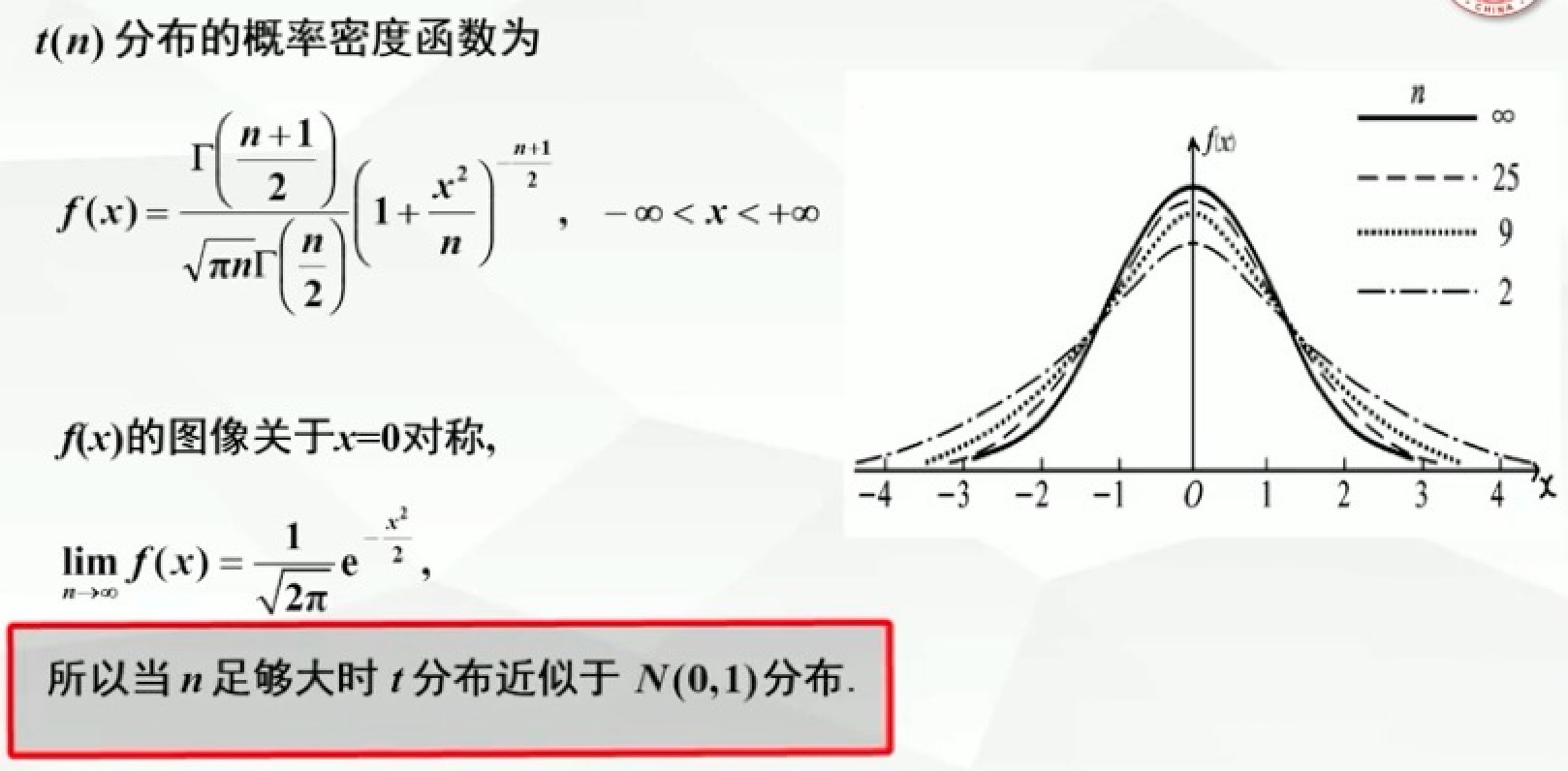
t分布例题
F分布

设U~X²(n1)，V~X²(n2)，且U与V相互独立，则称F=(U/n1) / (V/n2) 服从自由度为(n1,n2)的F分布，记为F~F(n1,n2)，其中n1称为第一自由度，n2称为第二自由度

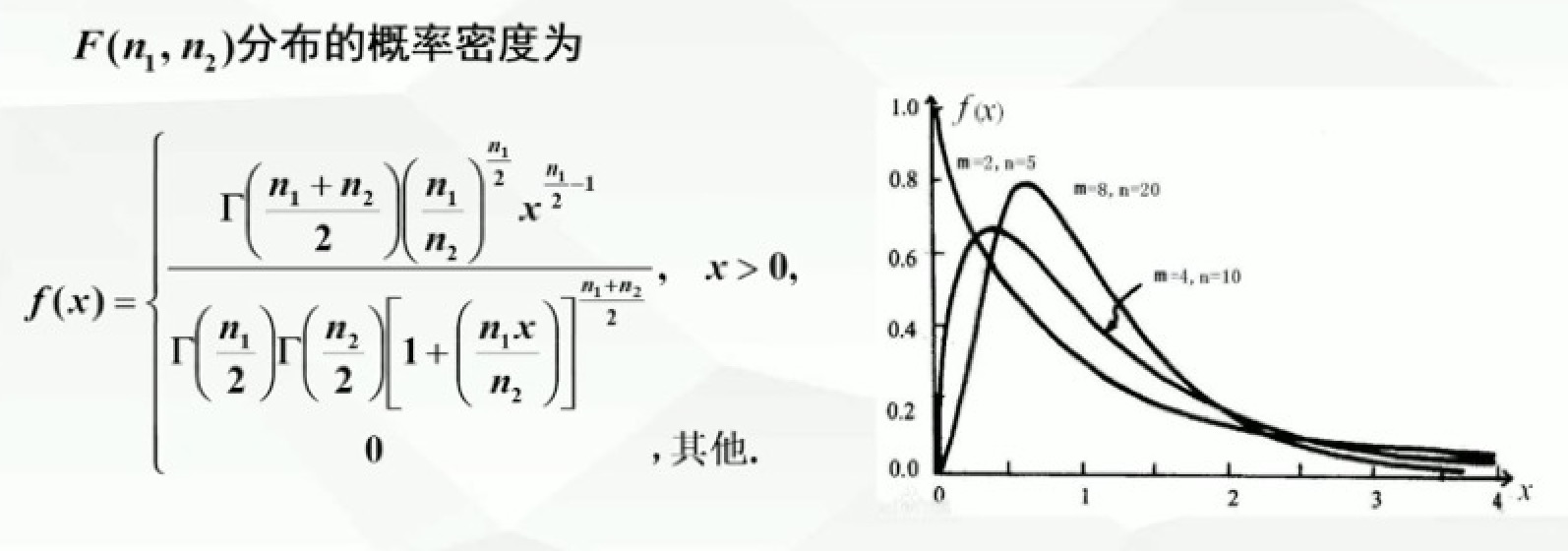
F分布例题
结论

若T~t(n)，则T²~F(1,n)

6.3.3 上（侧）α分位数

定义

对于随机变量X，给定α(0<α<1)，若存在数Xa，使得P{X＞Xa}=α，则称Xa为X（或它的分布）的上（侧）分位数，如下图所示
常见的几种分位数

1）标准正态分布的上（侧）α分位数

2）X²分布的上（侧）α分位数

3）t分布的上（侧）α分位数

4）F(n1,n2)分布的上（侧）α分位数
性质总结

1）Z(1-α) = -Z(α)

2）

$F_{1-a}(n_1,n_2)=\frac1{F_a(n_2,n_1)}$

6.3.4 抽样定理

定理一

设总体X~(μ,σ²)，X1,X2,…,Xn是样本，X平均和S²分别是样本均值和样本方差，则有结论

1）X平均~N(μ, σ²/no)

2）X平均与S²相互独立

3）(n-1)S²/σ² ~ X²(n-1) —> Σ(Xi-μ/σ) ~ X²(n)

推论

1）由结论1，可得 X平均-μ/(σ/根号n) ~ N(0,1)

2）X平均-μ/(S/根号n) ~ t(n-1)

定理二

设总体X~N(μ1,σ1²)，总体Y~N(μ2,σ2²)，X1,X2,…,Xn与Y1,Y2,…,Yn分别是来自两个总体的样本，并且这两个样本相互独立，样本均值分别为X平均和Y平均，样本方差分别是S1²和S2²，则有以下三个抽样分布

1）

$\frac{(\overline X - \overline Y)-(μ_1-μ_2)}{\sqrt{\frac{σ_1^2}{n_1}+\frac{σ_2^2}{n_2}}}～N(0,1)$

2）

$\frac{S_1^2/σ_1^2}{S_2^2/σ_2^2}～F(n_1-1,n_2-1)$

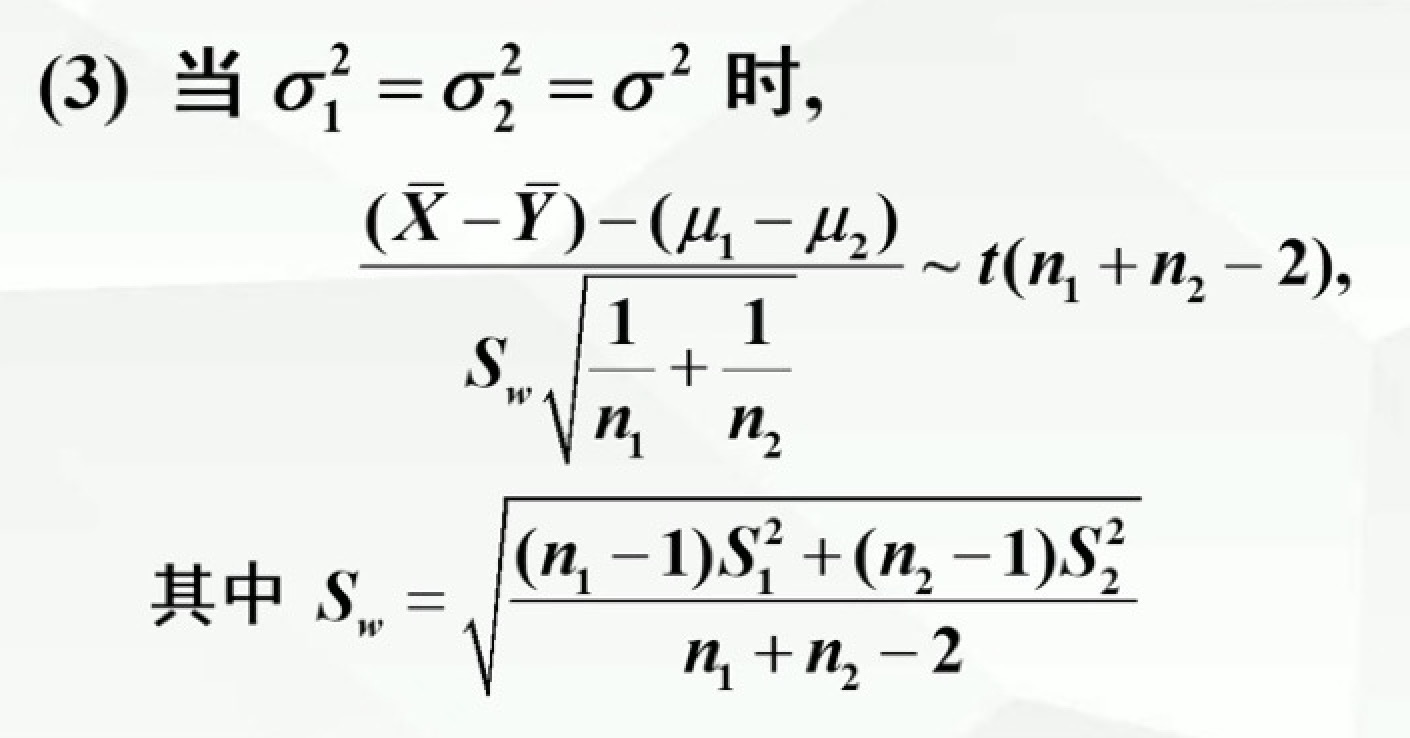
第七章参数估计

7.1 点估计

7.1.1 矩估计

统计推断

通过样本对总体的特征进行估计、推断或预测
参数

反映总体某些方面特征的量
点估计

点估计问题是要构造一个适当的统计量θ^ (X1,X2,…,Xn)，用它来估计未知参数θ，θ^ 则称为参数θ的点估计量

若给定一组样本观测值X1,X2,…,Xn则θ^ (x1,x2,…,xn)称为参数θ的点估计值
样本i阶矩是总体X的i阶矩的 矩估计

7.1.2 最大似然估计

似然函数

X1,X2,…,Xn是来自总体X的样本，x1,x2,…,xn为样本观测值

1）设总体X属离散型

设分布律P{X=x}=p(x;θ)，θ为待估参数，则样本X1,X2,…,Xn取到观测值x1,x2,…,xn的概率，P{X1=x1,X2=x2,…,Xn=xn}=L(θ)，称为样本似然函数

2）设总体X属连续型

设概率密度f(x;θ)，θ为待估参数，X1,X2,…,Xn是来自总体X的样本，则样本在观测值邻域发生的概率，可得

似然函数L(θ)=∏f(xi;θ)
说明

1）求L(θ)最大值点，为简化计算，通常求lnL(θ)最大值点，令dlnL(θ)/dθ=0

2）若L(θ)关于θ是单调递增(减)函数，则θ最大似然估计为θ最大(小)值，与样本有关

3）最大似然估计具有不变性
总结对参数求最大似然估计步骤

1）写似然函数

2）取对数lnL(θ)

3）令dlnL(θ)/dθ = 0，解θ的最大似然估计θ^

7.2 估计量的评选标准

无偏性准则

若参数θ的估计量θ^ = θ^ (X1,X2,…,Xn)，满足E(θ^ )=θ，则称θ^是θ的无偏估计量

1）其统计意义是在大量重复独立实验下，由θ^ (X1,X2,…,Xn)给出的估计的平均值恰好是参数θ

2）若E(θ^ ) ≠ θ，且limE(θ^ )=θ，则θ^称为θ的渐进无偏估计量

3）X平均是μ的无偏估计，S²是σ²的无偏估计，样本二阶中心距不是σ²的无偏估计，是渐进无偏估计
有效性准则

若θ^ 1和θ^ 2都是未知参数θ的无偏估计量，即E(θ^ 1)=E(θ^ 2)=θ，如果D(θ^ 1)≤D(θ^ 2)，则称估计量θ^ 1比θ^ 2有效

注意：方差较小的无偏估计量更有效
相合性准则

设θ^ =θ^ (X1,X2,…,Xn)为未知参数θ的估计量，若∀ε>0，有lim(n->∞){|θ^ -θ|≥ε}=0，则称θ^ 为θ的相合估计量

7.3 区间估计

7.3.1 置信区间

区间估计

估计一个范围，使之以较大的概率包含未知参数
定义

设总体X的分布函数F(x;θ)含有一个未知参数θ，对给定值α(0<α<1)，若由样本X1,X2,…,Xn确定的两个统计量θ^ 1和θ^ 2满足 P{θ^ 1(X1,X2,…,Xn)<θ<θ^ 2(X1,x2,…,Xn)}=1-α

则称随机区间(θ^ 1,θ^ 2)是θ的置信水平为1-α的(双侧)置信区间，θ^ 1和θ^ 2分别称为置信下限和置信上限，置信水平1-α也称为置信度
说明

1）被估计参数θ虽然未知，但它是一个常数，没有随机性

2）θ^ 1与θ^ 2是统计量，依赖于样本

3）置信区间(θ^ 1,θ^ 2)是随机区间，依赖于样本，样本值不同则算出来的区间不同

4）有些样本观测值算出的区间包含θ的真值，而有些则不包含
精确度：

置信区间长度L，L越大则精确度越低，置信度越大

置信区间长度L，L越小则精确度越高，置信度越小
Neyman原则

在保证置信度的条件下，选择精确度高的置信区间
求置信区间的步骤

1）寻求一个样本X1,X2,…,Xn的函数：G=G(X1,X2,…,Xn;θ)，G的分布已知且不依赖于任何未知参数

2）对于给定的置信度1-α，定出两个常数a,b，使P{a＜G＜b}=1-α

3）从a<G<b中解出θ，得到等价的不等式θ^ 1<θ<θ^ 2，即P{a<G＜b}=1-α <=> P{θ^ 1<θ＜θ^ 2}=1-α，那么(θ^ 1, θ^ 2) 就是θ的一个置信度为1-α的置信区间

7.3.2 单个正态总体均值、方差的置信区间

正态总体均值μ的置信区间

设总体X~N(μ,σ²)，X1,X2,…,Xn为来自总体X的样本，X平均，S²分别为样本均值和样本方差，设给定置信水平为1-α

1）σ²已知，X平均~N(μ, σ²/n)

X平均是μ的矩估计量，构造枢轴量Z=(X平均-μ)/(σ/根号n) ~ N(0,1)

置信区间如下，置信区间长度为L

$(\overline X±\fracσ{\sqrt{n}}Z_{α/2})$

当n固定时，

置信度1-α越大，Za/2越大，L越大，精确度越低；

置信度1-α越小，Za/2越小，L越小，精确度越高

2）σ²未知

S²是σ²的无偏估计量，构造枢轴量T=(X平均-μ)/(S/根号n) ~ t(n-1)

置信区间如下

$(\overline X±\frac{S}{\sqrt{n}}t_{α/2}(n-1))$
正态总体方差的置信区间（μ未知）

S²是σ²的无偏估计量，构造枢轴量X²=(n-1)S²/σ² ~ X²(n-1)

σ²的一个置信度为1-α的置信区间

$(\frac{(n-1)S^2}{X^2_{α/2}(n-1)},\frac{(n-1)S^2}{X^2_{1-α/2}(n-1)})$

7.3.3 两个正态总体均值差、方差比的置信区间

两正态总体均值差的置信区间

μ1μ2的置信区间

1）σ1²和σ2²已知，置信区间如下

$((\overline X-\overline Y)±z_{α/2}\sqrt{\frac{σ_1^2}{n_1}+\frac{σ_2^2}{n_2}})$

2）σ1²和σ2²未知且相等，置信度为1-α的置信区间如下

$((\overline X-\overline Y)±t_{α/2}(n_1+n_2-2)S_w\sqrt{\frac1{n_1}+\frac1{n_2}})$

两正态总体房差比的置信区间

σ1²/σ2²的置信区间（μ1, μ2未知）

$(\frac{S_1^2}{S_2^2}\frac1{F_{\frac a2}(n_1-1,n_2-1)},\frac{S_1^2}{S_2^2}\frac1{F_{1-\frac a2}(n_1-1,n_2-1)})$

7.4 单侧置信限

定义

设总体X的分布函数F(x;θ)含有一个未知参数θ，X1,X2,…,Xn是样本，若对给定值α(0<α<1)，存在统计量θ^ L=θ^ L(X1,X2,…,Xn)，满足P{θ^ L(X1,X2,…,Xn)<θ}=1-α，则称θ^ L是θ的置信水平为1-α的单侧置信下限（上限以此类推）

正态总体均值μ的单侧置信限

设总体X~N(μ,σ²)，X1,X2,…,Xn为来自总体X的样本，设给定的置信水平为1-α

1）σ²已知，μ的置信水平为1-α的单侧置信上下限为

$\overline X±\frac σ{\sqrt n}Z_α$

2）σ²未知，μ的置信水平为1-α的单侧置信上下限为

$\overline X±\frac S{\sqrt n}t_a(n-1)$

正态总体方差的单侧置信限

1）μ未知，σ²的置信水平为1-α的单侧置信下限

$\frac{(n-1)S^2}{X_a^2(n-1)}$

上限

$\frac{(n-1)S^2}{X_{1-α}^2(n-1)}$

第八章假设检验

Z-检验

检验假设H0:μ=μ0，H1:μ≠μ0，当σ²已知

$统计量\ μ=\frac{\overline X-μ}{σ/\sqrt n}$

T-检验

检验同上，但σ²未知，S为标准差

$统计量\ T=\frac{\overline X-μ}{S/\sqrt n}$