一.认识蓝桥杯赛制

  • 分组：大学A/B组，985、211高校只能报A组，其他学校自选

  • 题型

    • 结果填空题：解唯一，无需写出计算过程，可编程、计算器、Excel计算，填结果即可
    • 程序填空题：给出某一解法的代码，补全空缺部分
    • 编程大题：用到标准输入与标准输出，按题目要求格式给出解

  • C/C++组大题注意事项

    • 程序处理完数据后记得 return0，不要等待下一个用例输入
    • 解答要符合ANSI C++标准，不要乱调用API
    • 头部要明确#include <xxx>

  • 注意时间复杂度和空间复杂度

    1
    2
    3
    4
    5
    6
    7
    8
    o(1)		常数阶
    O(logn)		对数阶
    o(n)		线性阶
    o(nlogn)	线性对数阶
    o(n²)		平方阶
    o(n³)		立方阶
    o(2^n)		指数阶
    o(n!)		阶乘阶

二.字符串和日期处理

输出图形

[大题]例1-打印规律金字塔

要求：当输入4或字母D时，分别输出以下图形

1
2
3
4
5
6
7
8
9
   1
  121
 12321
1234321

   A
  ABA
 ABCBA
ABCDCBA

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
using namespace std;

int main() {
    char c;
    cin >> c;
    if(c>='A' && c<='Z'){
        for(int i=1;i<=c-'A'+1;i++){
            //打印空格
            for(int j=1; j<=c-'A'+1-i; j++){
                cout<<" ";
            }
            //先打递增字母
            for(int j=1; j<=i; j++){
                cout<< (char)('A'+j-1);
            }
            //打印递减部分
            for(int j=i-1; j>=1;j--){
                cout<< (char)('A'+j-1);
            }
            cout << endl;
        }
    }else{
        for(int i=1;i<=c-'1'+1;i++){
            //打印空格
            for(int j=1; j<=c-'1'+1-i; j++){
                cout<<" ";
            }
            //先打递增字母
            for(int j=1; j<=i; j++){
                cout<< (char)('1'+j-1);
            }
            //打印递减部分
            for(int j=i-1; j>=1;j--){
                cout<< (char)('1'+j-1);
            }
            cout << endl;
        }
    }
    return 0;
}
/*总结：主要考察ASCII码的应用*/

[大题]例2-造房子

假设*为宝藏，我们要建房子保护它

要求输入宝藏布局m(行)和n(列），当输入3 4时输出如下

1
2
3
4
5
6
7
+-+-+-+-+
|*|*|*|*|
+-+-+-+-+
|*|*|*|*|
+-+-+-+-+
|*|*|*|*|
+-+-+-+-+

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
using namespace std;

int main() {
    int n,m;
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cout<<"+-";
        }
        cout << "+"<< endl;
        for(int j=1;j<=m;j++){
            cout<<"|*";
        }
        cout << "|"<< endl;
    }
    for(int j=1;j<=m;j++){
        cout<<"+-";
    }
    cout << "+"<< endl;
    return 0;
}

/*总结：此题要点为观察+-符号和宝藏的关系，较简单*/

字符串处理

  • C++常用的字符串处理函数：
    • strcpy(x,y)，将y字符串复制到x
    • strcat(x,y)，将y字符串拼接到x后面
    • strcmp(x,y)，每个字符依次比较，完全相等返回0，否则返回第一个差值
    • strlen(x)，获取字符串x的长度，注意最好不要放在循环条件里（时间开销大）

[填空]例3-对称是一种美

要求输入与输出如下所示

输入1时，输出A

输入2时，输出ABA

输入3时，输出ABACABA

输入4时，输出ABACABADABACABA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <string.h>

char res[5000000];
int main() {
    int n;
    scanf("%d",&n);
    int len = 0;
    for(int i=1; i<=n; i++){
      
        /*在此处完善代码*/
      
        res[len] = 'A'+i-1;
        len = strlen(res);
    }
    printf("%s\n",res);
    return 0;
}

参考代码

1
2
strcat(res+len+1, res);
/*总结：此题考察了数组名与指针的关系，以及字符串拼接*/

[大题]例4-寻找字符串

有一个字符串为aba，可得它在另一个字符串abababa出现了3次，输入包含两行，第一行为被搜索的字符串(abababa)，第二行为要搜索的字符串(aba),字符串长度不大于1000，输出出现次数

输入样例

1
2
ossosso
osso

输出

1
2

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<cstdio>
#include<cstring>
char s1[1005], s2[1005];
int main() {

    fgets(s1, 1004, stdin); //fgets()是个坑，会读取换行符，可以换gets函数
    fgets(s2, 1004, stdin);
    int len1 = strlen(s1) - 1, len2 = strlen(s2) - 1;  //除去换行符
    int ans = 0;
    for(int i=0; i+len2-1 < len1; i++){
        bool matched = true;
        for(int j=0; j<len2;j++){
            if(s1[i+j]!=s2[j]){
                matched = false;
                break;
            }
        }
        if(matched){
            ans++;
        }
    }
    printf("%d\n",ans);
    return 0;
}

日期处理

  • 闰年的定义：

    • 年份非百且能被4整除的年份
    • 能被400整除的年份
    1
    if(year%400==0 || (year%100!=0 && year%4==0))

  • 快速计算星期几（不太可能记下来）

    1
    2
    3
    4
    /*蔡基姆拉尔森计算公式 y/m/d代表年月日*/
    w = (d+2*m+3*(m+1)/5 +y+y/4-y/100+y/400)%7
    w = w+1
    //注意1，2月当做上一年13、14月计算

[填空]例5-推算星期几

输入年、月、日，推算出那天是星期几

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>
#include <string>
using namespace std;
int whatday(int y, int m, int d){
    
  //补全代码，返回正确的星期,用0-6表示星期一到星期天
    
}
string weekday[7] = {"Monday","Tuesday","Wednesday","Thursday","Friday","Saturday","Sunday"};
int main() {
    int y,m,d;
    cin >> y >> m >> d;
    cout << weekday[whatday(y,m,d)] << endl;
    return 0;
}

参考代码 常见解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int ans = 0;
for (int i=1; i<y; i++){
  if(( i%100!=0 && i%4==0 ) || i%400==0){
    ans += 366%7;
    ans %= 7;
  }else{
    ans += 365%7;
    ans %= 7;
  }
}
for(int i=1; i<m; i++){
  if(i==1 || i==3 || i==5 || i==7 || i==8|| i==10|| i==12){
    ans += 31%7;
    ans %= 7;
  }else if(i==4 || i==6 || i==9 || i==11){
    ans += 30%7;
    ans %= 7;
  }else if((y%100!=0 && y%4==0) || i%400 ==0){
    ans += 29%7;
    ans %= 7;
  }else{
    ans += 28 % 7;
    ans %=7;
  }
}
ans += (d-1) % 7;
ans %= 7;
return ans;

[大题]例6-求纪念日

输入4个整数y,m,d,k表示一对情侣在一起的日期，求他们k天纪念日具体是哪一天？

输入样例

1
2016 10 1 100

输出样例

1
2017-01-09

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <cstdio>
//用数组表示每个月份天数（闰年2月另算）
int day[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};
int main() {
    int y,m,d,k;
    scanf("%d%d%d%d",&y,&m,&d,&k);
    for(int i=1; i<=k; i++){
        if((y%100!=0 && y%4==0) || y%400 == 0 ){
            day[2] = 29;
        }else{
            day[2] = 28;
        }

        if(d == day[m]){
            d = 1;
            m++;
            continue;   //注意这个continue的用途，防止d再次++
        }
        if(m == 13){
            m = 1;
            y++;
        }
        d++;
    }
    printf("%0d-%02d-%02d\n", y, m, d);
    return 0;
}

/*总结：考察闰年的判断、月份天数，注意continue的坑*/

综合练习

综合1-统计字符串 [*]

输入一个字符串(小于100个字符)，统计其中A的数量并输出

输入样例

1
fdAdAkljfJNnA

输出样例

1
3

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<cstdio>
#include<cstring>

char s[105];
int main() {

    int len, cnt=0;
    scanf("%s",s);
    len = strlen(s);
    for(int i=0; i<len; i++){
        if(s[i]=='A'){
            cnt++;
        }
    }
    printf("%d\n",cnt);
    return 0;
}
/*此题考查strlen函数和字符转换ASCII码方法，较简单*/

综合2-找最长字符串[*]

输入格式：第一行为输入的字符串个数N (0<N<100)

接下来N行是不同字符串

1
2
3
3d
hello
a

输出格式：输出最长的字符串

1
hello

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<cstdio>
#include<cstring>
char s[105], ans[105];
int anslen = 0;
int main() {

    int N, len;
    scanf("%d", &N);
    for(int i =0;i <N; i++){
        scanf("%s",s);
        len = strlen(s);
        if (len > anslen){
            anslen = len;
            strcpy(ans, s);
        }
    }
    printf("%s\n",ans);
    return 0;
}

/*此题主要考查strcpy函数，较简单*/

综合3-修改字符串[*]

输入一个长度大于10小于1000的字符串，要求把所有大小写字母改成下一个字母，如z改成a，Z改成A，其他字符不变

输入样例

1
Afd6gVBZaf4

输出样例

1
Bge6hWCAbg4

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <cstdio>
#include <cstring>

char s[1005];
int main() {
    int len;
    scanf("%s", &s);
    len = strlen(s);
    for(int i =0; i<len; i++){
        if(s[i] == 'z'){
            s[i] = 'a';
        }else if(s[i] == 'Z'){
            s[i] = 'A';
        }else if(s[i]>='A' && s[i]<='Z' || s[i]>='a' && s[i]<='z'){  //注意这里的判断条件，容易忽略
            s[i]++;
        }

    }
    printf("%s\n",s);
    return 0;
}

综合4-判断超级偶数 [**]

从键盘输入一个位数最多达到10000的整数（long long也存不下），判断他是不是偶数，是则输出YES，否则输出NO

输入样例

1
3242398979

输出样例

1
NO

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <cstdio>
#include <cstring>
char s[10005];
int main() {
    int len;
    scanf("%s", &s);
    len = strlen(s);
    if((s[len-1] - '0')%2 == 0){
        printf("YES\n");
    }else{
        printf("NO\n");
    }
}
/*此题技巧是将数字按字符串来处理取出末位，比较巧妙*/

综合5-字符倒序输出[*]

输入样例

1
1234567890

输出样例

1
0987654321

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include<cstdio>
#include<cstring>

char s[100005];
int main() {
    int len ;
    scanf("%s", s);
    len = strlen(s);
    for(int i = len -1;i>=0;i--){
        printf("%c",s[i]);
    }
    printf("\n");
    return 0;
}
/*考查字符串和字符的关系，数组长度一般小于10^5不会超限*/

综合6-输出最后单词长度[**]

输入一行字符串s，长度不超过10000

1
Welcome to 515code

输出最后一个单词长度

1
7

参考代码

1
2
3
4
5
6
7
8
9
#include<cstdio>
#include<cstring>
char s[10005];
int main(){
    while(scanf("%s",&s)!=EOF);
    printf("%d\n",strlen(s));
    return 0;
}
/*此题值的一看，使用了EOF的小技巧，scanf在读取到空格时会停止并重新读取下一个，因此while循环实际上读到的是最后一个单词*/

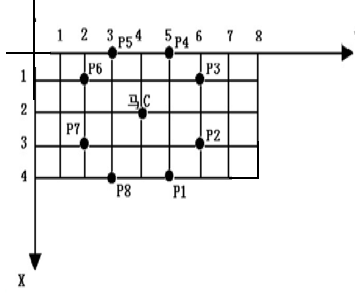
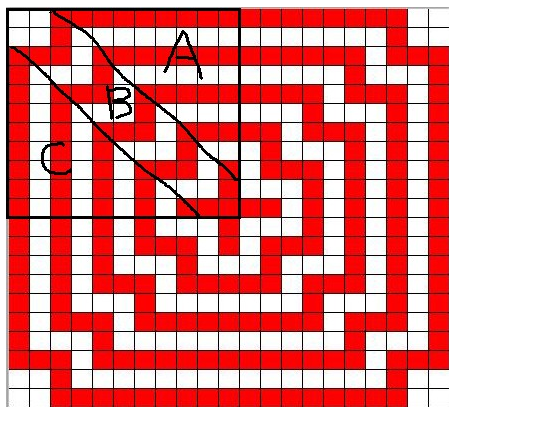
综合7-真题-打印十字图[***]

小明为某机构设计了一个十字型的徽标。

输入格式

一个正整数 n (n<30) 表示要求打印图形的层数。

输出格式

对应包围层数的该标志

输入样例

1
1

输出样例

1
2
3
4
5
6
7
8
9
..$$$$$..
..$...$..
$$$.$.$$$
$...$...$
$.$$$$$.$
$...$...$
$$$.$.$$$
..$...$..
..$$$$$..

输入样例

1
3

输出样例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
..$$$$$$$$$$$$$..
..$...........$..
$$$.$$$$$$$$$.$$$
$...$.......$...$
$.$$$.$$$$$.$$$.$
$.$...$...$...$.$
$.$.$$$.$.$$$.$.$
$.$.$...$...$.$.$
$.$.$.$$$$$.$.$.$
$.$.$...$...$.$.$
$.$.$$$.$.$$$.$.$
$.$...$...$...$.$
$.$$$.$$$$$.$$$.$
$...$.......$...$
$$$.$$$$$$$$$.$$$
..$...........$..
..$$$$$$$$$$$$$..

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <cstdio>
char s[125][125];   //4n+5行列，当n=30时为125，节省空间
int main(){
    int n;
    scanf("%d",&n);

    //遍历表盘为'.'
    for(int i=0;i<4*n+5; i++){
        for(int j=0;j<4*n+5; j++){
            s[i][j] = '.';
        }
    }

    //先打十字 中心坐标[2n+2][2n+2]
    int center = 2*n+2;
    s[center][center] = '$';
    for(int i=1;i<=2;i++){
        s[center+i][center] = '$';
        s[center-i][center] = '$';
        s[center][center+i] = '$';
        s[center][center-i] = '$';
    }
    //打印包围圈
    for(int i=1;i<=n;i++){
        //左上角
        int k=center-2*i;
        int m=center-2*i-2;
        s[k][m+1]='$';
        s[k][m+2]='$';
        s[k-1][m+2]='$';
        //上方
        for(int j=1;j<=4*i+1;j++){
            s[k-2][m+2+j-1]='$';
        }
        //左方
        for(int j=1;j<=4*i+1;j++){
            s[k+j-1][m]='$';
        }
        //右上角
        k=center-2*i;
        m=center+2*i+2;
        s[k][m-1]='$';
        s[k][m-2]='$';
        s[k-1][m-2]='$';
        //右方
        for(int j=1;j<=4*i+1;j++){
            s[k+j-1][m]='$';
        }
        //左下角
        k=center+2*i;
        m=center-2*i-2;
        s[k][m+1]='$';
        s[k][m+2]='$';
        s[k+1][m+2]='$';
        //下方
        for(int j=1;j<=4*i+1;j++){
            s[k+2][m+2+j-1]='$';
        }
        //右下方
        k=center+2*i;
        m=center+2*i+2;
        s[k][m-1]='$';
        s[k][m-2]='$';
        s[k+1][m-2]='$';
    }
    //输出图像
    for(int i=0; i<4*n+5; i++){
        printf("%s\n",s[i]);
    }
    return 0;
}
/*此题考查图像规律，下面详细解释我的算法*/

此题看着输出像一个长方形，但画出来后发现其实是正方形

十字图

首先，把表盘遍历为 '.'符号

第一步：先定位中心点，把5*5的十字打印出来

第二步：定位这四个点，打印十字外一侧红色包围圈

其中用到等差数列原理，不过不知道我的这个算法空间、时间会不会超限。

综合8-计算一年放假多少天[***]

日历有 阳历（公历） 和 阴历（农历） 之分。每年都有法定节假日，这些分成三类——双休、阳历节假日、阴历节假日。

1.双休

周六和周日 2 天

2.阳历节假日

1）元旦：阳历每年 1 月 1 日，放假 1 天

2）劳动节：阳历每年 5 月 1 日，放假 1 天

3）国庆节：阳历每年 10 月 1 日，放假 3 天

4）圣诞节：阳历每年 12 月 25 日，放假 1 天 3.阴历节假日

1）春节：阴历每年 1 月 1 日，放假 3 天

2）清明节：阳历每年 4 月 4 - 6 日之间的某天，放假 1 天

3）端午节：阴历每年 5 月 5 日，放假 1 天

4）中秋节：阴历每年 8 月 15 日, 放假 1 天

当节假日和双休重合时，双休 不延后 也 不提前，保证节假日之间不会重合。现在给你某年的所有阴历节假日的 阳历 日期，以及当年的 1 月 1 日是星期几，请你计算出这一年（阳历 1 月 1 日到 12 月 31 日）放了多少天假（包括双休、阳历节假日和阴历节假日）。

输入格式

第一行输入年份y(1900<y≤2050)。

接下来 4 行，每行输入两个整数 m,d, 依次表示春节、清明节、端午节和中秋节的阳历日期。 最后一行一个整数表示当年 1 月 1 号是星期几（一周内的第几天，每周从星期一开始计数，即星期一为第一天）。

1
2
3
4
5
6
2017
1 28
4 4
5 30
10 4
7

输出格式

输出一个整数，表示当年放假的天数。

1
113

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <cstdio>
int day[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};  //写入每月天数，2月要做判断
int mm[10] = {1, 5, 10, 10, 10, 12};    //固定放假的月份
int dd[10] = {1, 1, 1, 2, 3, 25};    //对应上一个数组放假的日期
int nextday(int &m, int &d){
    if(d == day[m]){
        m++;
        d = 1;
    }else{
        d++;
    }
}
int main() {
    int y, w, m, d, f, ans;
    scanf("%d", &y);

    //若为闰年要给2月加一天
    if(y%4==0 && y%100!=0 || y%400==0){
        day[2] = 29;
    }
    //读取四行 春节 清明节 端午节 中秋节的阳历日期
    for (int i=6; i<10; i++){
        scanf("%d%d", &mm[i], &dd[i]);
    }
    //读取当年1月1号是星期几
    scanf("%d", &w);
    m = 1;
    d = 1;
    f = 0;
    ans = 0;
    while(m != 13){
        //判断春节
        if(m == mm[6] && d == dd[6]){
            ans++;
            f = 2;
        }else if(f){
            ans++;
            f--;
        }else if( w==6 || w==7){
            ans++;  //周末
        }else{
            for(int i=0; i<10; i++){
                //找节日
                if(m == mm[i] && d == dd[i]){
                    ans++;
                    break;
                }
            }
        }
        //下一天是几月几号
        nextday(m, d);
        //下一天星期+1
        w = w + 1;
        if(w == 8){
            w = 1;
        }
    }
    printf("%d\n",ans);
    return 0;
}

三.使用Sort排序（C++）

  • 若对一个数组元素进行交换，例如元素按顺序排序，我们可以使用C++的强大工具——sort

  • 头文件 #include <algorithm>

  • 举例：sort(arr, arr+5)，代表排序arr[0]到arr[4]，因此注意sort后面要多写一位

  • sort的参数

    1
    2
    3
    // 第三个参数为排序方法,grater代表从大到小排序
    // 若不填第三个参数，则默认从小到大排序
    sort(arr, arr+5, greater<int>)

[大题]例1-计算班级前K名平均成绩[*]

输入格式，一共输入三行

第一行：班级人数N (1到30人)

第二行：为N个分数 (整数)，用空格隔开

第三行：计算前K名分数的人数K

1
2
3
10
93 85 77 68 59 100 43 94 75 82
4

输出格式：输出前K名同学的分数平均数，四舍五入保留两位小数

1
93.00

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <cstdio>
#include <algorithm>
using namespace std;    //用greater排序要加这行
int score[31];
int main() {
    int N, K, sum;
    scanf("%d", &N);
    for(int i=0; i<N; i++){
        scanf("%d", &score[i]);
    }
    scanf("%d", &K);
    sort(score, score+N, greater<int>());
    sum = 0;
    for(int i=0; i<K; i++){
        sum += score[i];
    }
    printf("%.2f\n", 1.0*sum/K);	//注意输出格式，保留两位小数
    return 0;
}

[大题]例2-分数段统计[*]

老师想进行班级名次排序和各分数段的人数统计工作。

要求将N名同学的考试成绩放在A数组中，各分数段的人数放在B数组中：成绩为100的人数存到b[1]中，成绩90到99的人数存在b[2]中，成绩80到89的人数存在b[3]中，成绩70到79的人数存到b[4]中，成绩60到69的人数存在b[5]中，成绩60以下的人数存在b[6]中。

输入格式：共两行

第一行：班级人数N (1到30)

第二行：N个分数（整数），用空格隔开

1
2
10
93 85 77 68 59 100 43 94 75 82

输出格式：若干行

前N行：每行一个整数，为从高到低排序的分数

最后一行：各个分数段人数，即按顺序输出b数组

1
2
3
4
5
6
7
8
9
10
11
100
94
93
85
82
77
75
68
59
43
1 2 2 2 1 2

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <cstdio>
#include <algorithm>
using namespace std;    //用greater排序要加这行
int score[31];
int b[7];
int main() {
    int N;
    scanf("%d",&N);
    for(int i=0; i<N; i++){
        scanf("%d",&score[i]);
    }
    //排序
    sort(score,score+N,greater<int>());
    //输出N行排序后的分数
    for(int i=0; i<N; i++){
        printf("%d\n",score[i]);
    }
    for(int i=0; i<N; i++){
        if(score[i] == 100){
            b[1]++;
        }else if(score[i] >= 90){
            b[2]++;
        }else if(score[i] >= 80){
            b[3]++;
        }else if(score[i] >= 70){
            b[4]++;
        }else if(score[i] >= 60){
            b[5]++;
        }else{
            b[6]++;
        }
    }
    //输出各分数段人数
    for(int i=1; i<=6; i++){
        //注意输出的空格，最后一个不输出空格
        if(i != 6){
            printf("%d ",b[i]);
        }else{
            printf("%d", b[i]);
        }
    }
    return 0;
}
/*此题考查sort中内置的greater排序方法，较简单*/

[大题]例3-自定义排序方法[*]

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
#include <algorithm>
using namespace std;    //用greater排序要加这行
bool cmp(int x, int y){
    return x>y;		//注意不要用≥，会造成一些错误
}
int main() {
    int arr[10];
    for(int i=0;i<10;i++){
        cin >> arr[i];
    }
    sort(arr, arr+10, cmp);	//传入自定义排序cmp方法
    for(int i=0; i<10; i++){
        cout << arr[i] << " ";
    }
    cout << endl;
    return 0;
}
/*自己实现了一个greater排序方法*/

[大题]例4-整数的余数排序[*]

现有N个正整数，均小于10000。现在需要将这些正整数按照除以3的余数从小到大排序。即除以3余0的数排在除以3余1的数前面，如果余数相等则按照正整数值从小到大排序。

输入格式为两行

第一行：一共整数的个数N 0<N<101

第二行：用空格隔开的N个正整数，均小于10000

输出格式

一行，按题目要求排序后的N个正整数，用空格隔开

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<cstdio>
#include<algorithm>
using namespace std;
int num[105];
bool cmp(int x, int y){     //自定义排序函数
    if(x % 3 != y % 3){
        return x % 3 > y % 3;
    }else{
        return x < y;
    }
}
int main(){
    int N;
    scanf("%d", &N);
    for(int i=0; i<N; i++){
        scanf("%d",&num[i]);
    }
    sort(num, num+N; cmp);
    for(int i=0; i<N; i++){
        if(i != N-1){
            printf("%d ", num[i]);
        }else{
            printf("%d\n", num[i]);  //注意最后一个元素不要输出空格
        }
    }
}
/*学会写自定义的排序函数会让此题变得十分简单*/

[大题]例5-结构体排序说明[*]

假设我们要以结构体保存学生名字与4科分数，我们怎么按名字排序（长短），又怎么按4科分数依次排序呢？

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;

struct Student{
    string name;
    int score[4];
};

//实际上我们可以定义多个比较方法，需要时再去调用
bool cmp_name(Student x, Student y){
    return x.name < y.name;
}

bool cmp_score(Student x, Student y){
    if(x.score[0]!=y.score[0]){
        return x.score[0] > y.score[0];
    }
    if(x.score[1]!=y.score[1]){
        return x.score[1] > y.score[1];
    }
    if(x.score[2]!=y.score[2]){
        return x.score[2] > y.score[2];
    }
    if(x.score[3]!=y.score[3]){
        return x.score[3] > y.score[3];
    }
}
int main() {
    Student stu[3];
    for(int i=0; i<3; i++){
        cin >> stu[i].name;
        for(int j=0; j<4; j++){
            cin >> stu[i].score[j];
        }
    }
    sort(stu, stu+3, cmp_score);
    for(int i=0; i<3; i++){
        cout << stu[i].name << ": ";
        for(int j=0; j<4; j++){
            cout << stu[i].score[j] << " ";
        }
        cout << endl;
    }

    return 0;
}

[大题]例6-排序评奖-结构体[**]

假设所在班级有N名同学，期末考试进行了语数英、体育四门课程考试，班主任要将这N名学生中总分前3名定为本学期的 ”学习标兵“。现给出这N名学生的姓名和各科成绩，请你编程找到总分前三名，并依次输出他们的姓名，所给数据不会出现总分相同情况。

输入格式

输入包含N+1行，第一行有一个正整数N表示班级人数 (3到40人)，接下来N行为每个学生的考试信息，依次为：姓名、数学成绩、语文成绩、英语成绩和体育成绩，用空格隔开。注意姓名都用小写字母（不超过10个），成绩为不超过200的非负整数。

1
2
3
4
5
4
jing 98 90 87 74
ming 96 92 85 97
jun 95 78 56 91
hong 95 100 85 78

输出格式

输出包含三行，分别是第一名到第三名同学的名字

1
2
3
ming
hong
jing

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <cstdio>
#include <algorithm>
using namespace std;

struct Student{
    char name[15];
    int score[4];
};

bool cmp(Student x, Student y){
    int sumx = x.score[0] + x.score[1] +x.score[2] +x.score[3];
    int sumy = y.score[0] + y.score[1] +y.score[2] +y.score[3];
    return sumx > sumy;
}

Student stu[45];
int main(){
    int N;
    scanf("%d",&N);
    for(int i=0; i<N; i++){
        scanf("%s", stu[i].name);
        for(int j=0; j<4; j++){
            scanf("%d", &stu[i].score[j]);
        }
    }
    sort(stu, stu+N, cmp);
    for(int i=0; i<3; i++){
        printf("%s\n",stu[i].name);
    }
    return 0;
}
/*此题主要考察结构体的定义及sort排序方法*/

注意：班级排序的若要按姓名排序，使用strcmp(a,b)<0即可，这个函数返回值意义是若a排在前面，则返回一个差值，这个差值小于0

[大题]例7-浮点数排序[**]

假设有N个正浮点数，均小于10000.0，现在需要将这些浮点数按照距离它最近的整数的差从小到大排序。浮点数与距离最近的整数的差越小，这个浮点数排位便越靠前，若差相等，按照浮点数值从小到大排序。

判断浮点数相等使用如下语句

1
2
3
if(fabs(a-b) < EPSILON){
	//执行两个浮点数相等时的操作，其中EPSLION为常量=10^-6
}

输入格式

一共两行，第一行为一个整数N (0到100)

第二行为空格隔开的N个正浮点数

1
2
9
1.001 2.1 3.2 4.0001 5.000001 6.9 7.2 8.001 9.0

输出格式

输出一行，为按题目要求排序后的N个正浮点数，四舍五入保留6位小数，按空格隔开。

1
9.000000 5.000001 4.000100 1.001000 8.001000 2.100000 6.900000 3.200000 7.200000

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const double EPSLION = 1e-6;
double num[105];

bool cmp(double a, double b){
    double da = fabs(a - round(a));	//round函数为四舍五入浮点数
    double db = fabs(b - round(b));	//fabs函数为求绝对值
    if(fabs(da-db) < EPSLION){
        return a < b;
    }
    return da < db;
}
int main(){
    int N;
    scanf("%d", &N);
    for(int i=0; i<N; i++){
        scanf("%lf", &num[i]);
    }
    sort(num, num+N, cmp);
    for(int i=0; i<N; i++){
        if(i!=N-1){
            printf("%lf ", num[i]);//不指定保留几位默认6位
        }else{
            printf("%lf\n", num[i]);
        }
    }
    return 0;
}

/*此题除了考查sort排序，还考察了math模块下的fabs和round函数*/
//顺便说下C++中快速四舍五入保留n位有效数字的方法
cout<<setiosflags(ios::fixed)<<setprecision(1); //四舍五入保留1位
cout << 2.56;	//输出结果为2.6

[大题]例8-分数线[**]

某学校举办了一场计算机竞赛选拔赛，现在大家的成绩已经出来了。老师需要确定决赛名单。

为了鼓励大家，老师希望获奖人数不少于参赛总人数的一半，因此老师需要确定一个获奖分数线，在分数线及以上的同学可以获奖，除此之外，分数线越高越好。

输入格式：

第一行：一个整数n，表示参赛总人数（0到10000）

第二行：n个参赛同学的分数（整数），用空格隔开

1
2
7
76 71 42 4 27 27 20

输出格式：

输出一行，包括两个整数，分别为分数线和获奖人数，用空格隔开

1
27 5

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <cstdio>
#include <algorithm>
using namespace std;

int score[10001];
int main(){

    int n;
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        scanf("%d",&score[i]);
    }
    sort(score,score+n, greater<int>());
    printf("%d ",score[(n-1)/2]);		//找中位数

    int cnt = 0;
    for(int i=0; i<n; i++){
        if(score[i] >= score[(n-1)/2]){
            cnt++;
        }else{
            break;
        }
    }
    printf("%d\n", cnt);
    return 0;
}
/*此题考查基本的sort方法，求中位数的方法*/

[大题]例9-红绿蓝珠子[**]

有一个罐子，里面装着红、绿、蓝色的玻璃珠若干，分别用R G B表示。现希望把他们排成一行，按照字典顺序排列（B->G->R），然后以一红二绿三蓝为一组串成一串幸运珠，多余的放回罐子中，那么能串多少串幸运珠呢？

输入格式

输入为一行，由若干个R G B乱序组成的字符串，长度小于10000，每个字母至少出现一次

1
RGGBBB

输出格式

第一行：排序完成后的字符串

第二行：一个整数，为串成的幸运珠条数

1
2
BBBGGR
1

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
char s[10005];
int main(){
    int len, r, g, b;
    scanf("%s",&s);
    len = strlen(s);
    sort(s, s+len);
    printf("%s\n", s);
    r = 0;
    g = 0;
    b = 0;

    for(int i=0; i<len; i++){
        if(s[i] == 'R'){
            r++;
        }else if(s[i] == 'G'){
            g++;
        }else{
            b++;
        }
    }
    printf("%d\n", min(r, min(g/2, b/3)));  //巧妙运用min函数
    return 0;
}
/*除了考查排序外，还考察了组合问题，实际上是求珠子的限制量（最小值）*/

[大题]例10-整数排序进阶[**]

有N个正整数均小于10000，现在要将这些正整数每一位数字相加的和从小到大排序。若各位相加相等，则按正整数值从小到大排序。

输入格式：

第一行为一个整数N （0<N<101）

第二行为用空格隔开的N个正整数

1
2
4
20 12 1 11

输出格式：

一行，为排序后N个正整数，用空格隔开

1
1 11 20 12

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <cstdio>
#include <algorithm>
using namespace std;
int num[105];
bool cmp(int a, int b){
    int suma=0,sumb=0;
    int tempa = a, tempb = b;
    while(a){
        suma += a%10;
        a/=10;
    }
    while(b){
        sumb += b%10;
        b/=10;
    }
    if(suma==sumb){
        return tempa<tempb;
    }
    return suma<sumb;
}
int main(){
    int N;
    scanf("%d", &N);
    for(int i=0; i<N; i++){
        scanf("%d", &num[i]);
    }
    sort(num, num+N, cmp);
    for(int i=0; i<N; i++){
        if(i!=N-1){
            printf("%d ",num[i]);
        }else{
            printf("%d",num[i]);
        }
    }
    return 0;
}
/*此题考查取位数的方法，即一个数对10取余，再除以10的反复循环*/

[大题]例11-抢气球[***]

小朋友下课在抢气球，每个气球在墙壁上有一定高度，当小朋友跳起来时，手能够到的高度要大于等于气球的高度才能摘下气球。为了公平，老师让跳的低的小朋友先跳。小朋友贪心，会把跳起来能摘到的气球全摘了。

很巧的是，每个小朋友跳起来手能够到的高度不一样。

输入格式：

第一行输入两个空格分隔的整数n,m(1≤n, m≤1000) ，n表示小朋友的数量，m表示气球的数量。

第二行输入n个正整数，用空格隔开，第i个数表示第i个小朋友能跳起来够着的高度ai(1≤ai≤10^5)

第三行输入m个正整数，用空格隔开，第i个数hi表示气球的高度(1≤hi≤10^5)

1
2
3
5 6
3 7 9 6 4
1 2 3 4 5 6

输出格式：

一共n行，每行一个整数，第i行表示第i个小朋友获得气球的数量

1
2
3
4
5
3
0
0
2
1

参考代码 算法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <cstdio>
#include <algorithm>
using namespace std;
struct Children{
    int a;  //能够到的高度
    int id; //编号
};
bool cmp(Children x, Children y){
    return x.a < y.a;
}

int ans[1005];	//存输出结果，小朋友摘了几个
int h[1005];		//存气球高度
bool used[1005];    //用来标记气球是否被摘
Children child[1005];
int main(){

    int n, m;
    scanf("%d%d",&n,&m);
    for(int i=0; i<n; i++){
        scanf("%d",&child[i].a);
        child[i].id=i;
    }
    for(int i=0; i<m; i++){
        scanf("%d",&h[i]);
    }
    sort(child, child+n, cmp);
    //摘气球
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            if(!used[j] && h[j]<=child[i].a){
                ans[child[i].id]++;
                used[j] = true;
            }
        }
    }

    for(int i=0; i<n; i++){
        printf("%d\n",ans[i]);
    }
    return 0;
}

参考代码 算法二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <cstdio>
#include <algorithm>
using namespace std;
struct Children{
    int a;  //能够到的高度
    int id; //编号
};
bool cmp(Children x, Children y){
    return x.a < y.a;
}

int ans[1005];	//存输出结果，小朋友摘了几个
int h[1005];	//存气球高度
Children child[1005];
int main(){

    int n, m, p;
    scanf("%d%d",&n,&m);
    for(int i=0; i<n; i++){
        scanf("%d",&child[i].a);
        child[i].id=i;
    }
    for(int i=0; i<m; i++){
        scanf("%d",&h[i]);
    }
    sort(child, child+n, cmp);
    sort(h, h+m);
    p=0;
    //摘气球
    for(int i=0; i<n; i++){
        while(p<m && h[p]<=child[i].a){
            ans[child[i].id]++;
            p++;
        }
    }

    for(int i=0; i<n; i++){
        printf("%d\n",ans[i]);
    }
    return 0;
}
/*注意此题要按小朋友编号输出，不是从矮到高排序输出*/

聪明的你想一想，上面两个算法哪个时间复杂度更低？

四.快速提升代码能力题解

  • 注意代码风格（缩进、空格、换行）

  • 来看看一些特别的题目吧~

例1-a+b问题

输入两个整数a，b，输出两个整数的和

输入格式：

第一行输入一个整数T，表示要计算的次数

接下来T行每行输入两个用空格隔开的整数a,b

1
2
3
4
5
6
5
1 2
3 4
5 6
7 8
9 10

输出格式

对于每次输入a,b，输出a+b的值，结果保证在32位整形(int)范围内

1
2
3
4
5
3
7
11
15
19

竞赛技巧：这里可以边读入边输出，不用连续读入再连续输出

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
#include <iostream>
using namespace std;
int main(){
    int T, a, b;
    cin >> T;
    for(int i=1; i<=T; i++){
        cin >> a >> b;
        cout<< a+b <<endl;
    }
    return 0;
}
/*小提示：cout和cin效率没有printf和scanf高，在处理大量数据的情况下要优先选择c语言*/

例2-斐波那契数列

相信大家学过斐波那契数列，它是1,1,2,3,5,8,13,21…

用fn表示斐波那契数列第n项，则f1=f2=1,fn=fn-1+fn-2(n>2)

输入一个n，求fn对(10^9+7)取模的结果

输入格式

输入一个整数n(1≤n≤100000)

1
3

输出格式

输出fn mod 1000000007的值

1
2

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>
using namespace std;
const int mod =1e9+7;
int f[10005];
int main(){
    int n;
    cin >> n;
    f[1] = 1;
    f[2] = 1;
    for(int i=3; i<=n; i++){
        f[i] = (f[i-1] + f[i-2])%mod;
    }
    cout << f[n] << endl;
    return 0;
}
/*这里采用了斐波那契数列的性质：后一个数对某个数取模等于 前两个数取模的结果相加 再对某个数取模，切勿将斐波那契数列一项项算出来，那样肯定超时间和空间*/

例3-矩阵旋转

给出一个n*m的整数矩阵，请你把这个矩阵顺时针旋转90°后输出

输入格式

第一行输入两个整数n, m (1≤n, m≤200)，用空格隔开

接下来n行，每行输入m个整数，表示输入的矩阵，矩阵中元素都是int范围整数

1
2
3
4
3 4
-1 3 6 3
7 7 9 1
10 3 4 6

输出格式

输出m行，每行n个空格隔开的整数，表示旋转后的矩阵。行末不要输出多余的空格。

1
2
3
4
10 7 -1
3 7 3
4 9 6
6 1 3

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;
int num[205][205];
int main(){
    int n, m;
    cin >> n >> m;
    for(int i=0; i<n; i++){
        for(int j=0;j<m;j++){
            cin >> num[i][j];
        }
    }
    for(int i=0; i<m; i++){
        for(int j=0; j<n; j++){
            if(j!=n-1){
                cout << num[n-1-j][i] << " ";
            }else{
                cout << num[n-1-j][i] << endl;
            }
        }
    }
    return 0;
}
/*将矩阵旋转90°，仔细观察可得到过程*/

例4-最大子阵

给定一个n*m的矩阵A，求A中的一个非空子矩阵，使这个子矩阵中元素的和最大。其中，A的子矩阵指在A中行和列均连续的一部分。

输入格式

输入第一行包括两个整数n,m(1≤n,m≤50)，分别表示矩阵A的行数与列数

接下来n行每行m个整数，表示矩阵Aij (-1000≤Aij≤1000)

1
2
3
4
3 3
2 -4 1
-1 2 1
4 -2 2

输出格式

输出一行，包含一个整数，为A中最大子矩阵的元素和

1
6

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
using namespace std;
int A[55][55];
int main(){
    int n, m, ans;
    cin >> n >> m;
    ans = -1005;
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin >> A[i][j];
        }
    }

    for(int i=0; i<n; i++){
        for(int j=i;j<n;j++){
            for(int k=0;k<m;k++){
                for(int l =k; l<m; l++){
                    int temp = 0;
                    for(int p = i;p <= j; p++){
                        for(int q=k; q<=l; q++){
                            temp+=A[p][q];
                        }
                    }
                    if(temp > ans){
                        ans = temp;
                    }
                }
            }
        }
    }
    cout << ans << endl;
    return 0;
}
/*不推荐这种最暴力的方法，后续动态规划会有讲到*/

例5-去重与排序随机数

n (1≤ n ≤ 1000 )个1到1000的随机整数，对于其中重复的数字，只保留一个，把其余相同的数去掉。然后再把这些数从小到大排序。

输入格式

第一行为一个正整数n

第二行有n个用空格隔开的正整数

1
2
10
20 40 32 67 40 20 89 300 400 15

输出格式

第一行输出一个整数m，表示不相同随机数的个数

第二行输出m个用空格隔开的正整数，为排序好的

1
2
8
15 20 32 40 67 89 300 400

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <algorithm>
using namespace std;
int num[105], ans[105];
int main(){
    int n;
    cin >> n;
    for(int i=0; i<n; i++){
        cin >> num[i];
    }
    sort(num, num+n);
    int m =0;
    //去重
    for(int i=0; i<n; i++){
        if(i!=0 && num[i] != num[i-1]){
            ans[m++] = num[i-1];
        }
    }
    //注意最后一位数不要漏掉
    ans[m++] = num[n-1];
    cout << m << endl;
    for(int i=0; i<m; i++){
        if(i != m-1){
            cout << ans[i] <<" ";
        }else{
            cout << ans[i] << endl;
        }
    }
    return 0;
}
/*此题注意去重时最后一个数的判断不要漏掉*/

例5-进制转换

输入一个十进制数N，将他转换为R进制数输出。在10≤R≤16的情况下，分别用ABCDEF表示。

输入格式

输入包含两个整数N(N<10000)和R(2≤R≤16)。注意N可能是负整数。

1
23 12

输出格式

输出一行，表示转换后的数字

1
18

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
using namespace std;
char ans[105];
int main(){
    int N, R, m=0, now;
    cin >> N >> R;
    if(N<0){
        cout << "-";
        N = -N;
    }
    while(N){
        now = N % R;
        if(now<=9){
            ans[m++] = '0' + now;
        }else{
            ans[m++] = 'A' + now - 10;
        }
        N /= R;
    }
  	if(m==0){
      cout << 0;
    }
    for (int i= m -1; i>=0; i--){	//倒序输出
        cout << ans[i];
    }
    cout << endl;
    return 0;
}
/*此题考查进制数转换过程，在数据结构的栈应用中有讲解*/

例6-回文数

一个正整数，若交换高低位以后和原数相等，那么称这个数为回文数。比如121，2332是回文数，而13，4567不是。

任意一个正整数，若其不是回文数，将该数交换高低位后和原数相加得到一个新的数。如果新数不是回文数，重复这个变换，直到得到一个回文数为止。例如，57变换后得到132 (57+75)，132得到363 (132+231)，361为回文数。

曾有数学家猜想：对于任意正整数，经过有限次上述变换后一定能得出一个回文数。

输入格式

第一行输入一个整数n

1
349

输出格式

第一行输出一个正整数，表示得到回文数的最少变换次数。接下来一行输出变换过程，用"—>"连接。保证最后生成的数在int范围内。

1
2
3
349--->1292--->4213--->7337

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
using namespace std;
int num[1005];
int digit[1005];
bool judge(int x){
    int cnt=0;
    while(x){
        digit[cnt++] = x%10;
        x/=10;
    }
    for(int i=0; i<cnt/2;i++){
        if(digit[i]!=digit[cnt-1-i])
            return false;
    }
    return true;
}
int rev(int x){
    int ret = 0;
    while(x){
        ret = ret*10+x%10;
        x/=10;
    }
    return ret;
}

int main() {
    int n, m=0;
    cin >> n;
    num[m++] = n;
    while(!judge(n)){
        n += rev(n);
        num[m++] = n;
    }

    cout << m-1 << endl;
    for(int i=0; i<m; i++){
        if(i!=m-1){
            cout << num[i] << "--->";
        } else{
            cout << num[i] <<endl;
        }
    }
    return 0;
}
/*此题考查数的反转、位数比较等知识点*/

例7-机器人

你在生日时收到了一份礼物，是一个智能机器人。这个机器人有四个指令：

1.forward x，前进x米

2.back x，先向后转，然后前进x米

3.left x，先向左转，然后前进x米

4.right x，先向右转，然后前进x米

现在把机器人放在坐标轴原点，起始朝向为x轴正方向。经过一系列指令后，你能计算出它的位置吗。坐标轴上一个单位长度为一1。

输入格式

第一行输入一个整数n(1≤n≤100)表示指令的个数。

接下来n行每行输入上面的指令，其中-1000≤x≤1000

1
2
3
4
5
6
7
8
9
10
11
10
back -9
left 3
left 8
back 15
right 10
right -7
right -3
left 11
right 17
left 3

输出格式

输出两个整数x,y表示机器人的最后坐标，用空格隔开。

1
9 -7

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
using namespace std;
int dx[4] = {0,-1,0,1};     //坐标系上左下右
int dy[4]={1,0,-1,0};
char op[15];
int main(){
    int n, d = 3,x,nowx,nowy;   //d为当前方向，即对应上面数组的右方向
    cin >> n;
    nowx = 0;
    nowy = 0;
    for(int i=0; i<n; i++){
        cin >> op >> x;
        if(op[0]=='b'){	//技巧：四个方向首字母不一样，可以此作为判断
            d = (d+2)%4;
        }else if(op[0]== 'l'){
            d = (d+1)%4;
        }else if(op[0] == 'r'){
            d = (d+3)%4;
        }
        nowx += dx[d] * x;
        nowy += dy[d] * x;
    }
    cout << nowx << " " << nowy <<endl;
    return 0;
}
/*此题考查数组和坐标系的结合应用，要注意机器人的当前方向*/

五.枚举算法

  • 能用枚举法解决的问题往往是最简单的一类题目，有以下共同特点
    • 解枚举的范围是有穷的
    • 检验条件是确定的

例1-找回文数字

观察数字：12321、123321都有个共同特点：无论从左往右还是从右往左读都是相同的，这样的数字叫回文数字。现在要从5位或6位十进制数字中找出各位数字之和等于n的回文数字。

输入格式

输入一个整数n (10≤n≤100)

1
50

输出格式

输出所有各个数之和等于n的5位和6位整数，每个数字一行，从小到大排序输出。若没有满足条件的数字输出-1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
799997
889979
889988
898889
898898
899969
899996
979979
988889
989969
989987
997799
998879
998897
999959
999995

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
using namespace std;
int n;
int digit[6];
bool judge(int x){
    int m = 0, sum = 0;
    while(x){
        digit[m++] = x%10;
        sum += x%10;
        x /= 10;
    }
    if(sum!=n){
        return false;
    }
    for(int i; i< m/2; i++){
        if(digit[i]!=digit[m-1-i]){
            return false;
        }
    }
    return true;
}
int main() {
    cin >> n;
    bool f = false;
    for(int i=10000; i<1000000; i++){
     if(judge(i)){
         cout << i << endl;
         f = true;
     }
    }
    if(!f){
        cout << -1 << endl;
    }
    return 0;
}
/*此题考查回文数的判断，较简单*/

例2-生日蜡烛

某人从某年开始每年举办一次生日Party，并且每次都要吹灭与他年龄数相同的根数的蜡烛。到现在他一共吹灭了236根蜡烛，那么他是几岁开始过生日Party的呢？假设这个人年龄不可能超过200岁。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <iostream>
using namespace std;
int main(){
    for(int i=1; i<=200; i++){
        int can = 0, j = i; //can为吹的蜡烛总数
        while(can < 236 && j< 200){
            can += j;
            j++;
        }
        if(can == 236){
            cout << i << endl;
        }
    }
    
    return 0;
}
/*在不能确定循环次数的情况下，优先使用while循环*/

例3-奖券数目

有人很迷信数字，比如带4的数字不吉利。某抽奖活动的奖券号码是5位数(10000~99999)，要求其中不带4的号码。主办方请你计算下，如果发行号码n到m之间的奖券，在任何两张奖券不重复的情况下，可发行多少张？

输入格式

输入一行，为空格隔开的两个整数n,m （10000≤n＜m≤99999)

1
10000 99999

输出格式

输出一个整数，为可发出奖券的数目

1
52488

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;
bool judge(int x){
    while(x){
        if(x%10==4){
            return true;
        }
        x/=10;
    }
    return false;
}
int main(){
    int n,m, cnt = 0;
    cin >> n >> m;
    for(int i=n; i<=m; i++){
        if(!judge(i)){    //返回true代表有4
            cnt++;
        }
    }
    cout << cnt << endl;
    return 0;
}
/*此题考查数字的拆分，较简单*/

六.常用STL（Standard Library）

vector数组

  • 假设想开一个数组，但是不确定长度，可以使用vector动态数组

  • 引用库

    1
    2
    3
    4
    5
    #include <vector>
    using namespace std;
    int main(){
        return 0;
    }

  • 构建动态数组：

    1
    2
    //其中a为数组名，T为类型名称，可以说int float double等等
    vector<T> a;

  • 插入元素（数组尾部）

    1
    2
    3
    4
    5
    6
    7
    8
    #include <vector>
    using namespace std;
    int main(){
        vector<int> vec;
        vec.push_back(1);	//[1]
        vec.push_back(2);	//[2]
        return 0;
    }

  • 获取长度

    1
    vec.size();

  • 访问元素和赋值方法与普通数组一样

  • 删除元素（最后一个元素）

    1
    vec.pop_back();

  • 清空并释放内存

    1
    2
    3
    //也可用clear方法，但这不会清空数组占用内存
    //vector<int> vec;
    vector<int>().swap(vec);

  • vector还可以存储自定义结构体

  • vector的构造函数快速初始化

    1
    vector<int> vec(n,1);	//第一个参数为初始化数组长度，第二个参数代表初始化数组值为1，不填默认为0

  • 用vector构造二维数组

    1
    2
    3
    vector<vector<int>> vec2;
    //构造一个n行m列二维数组,并全部初始化为0
    vector<vector<int>> vec2(n, vector<int>(m,0));

  • 下面试着打印一个以下效果的乘法口诀表试试吧！

    1
    2
    3
    4
    5
    1*1=1	
    2*1=2	2*2=4	
    3*1=3	3*2=6	3*3=9	
    4*1=4	4*2=8	4*3=12	4*4=16	
    5*1=5	5*2=10	5*3=15	5*4=20	5*5=25

    参考代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    #include <iostream>
    #include <vector>
    using namespace std;

    int main() {
        vector<vector<int>> v2d;
        for(int i=0; i<5; i++){
            v2d.push_back(vector<int>());
        }
        for(int i=0;i<v2d.size();i++){
            for(int j=0; j<=i; j++){
                v2d[i].push_back((i+1)*(j+1));
            }
        }
        for(int i=0; i<v2d.size();i++){
            for(int j=0; j<v2d[i].size(); j++){
                cout << i+1 << "*" << j+1<< "=" << v2d[i][j] << "\t";
            }
            cout << endl;
        }
        return 0;
    }

    ​

集合-set

集合是由不重复的数据构成的，例如{1,2,3}

C++中常用的是set

1
2
3
4
#include <set>
using namespace std;

set<T> s;

  • 插入元素 时间复杂度o(logn)

    1
    2
    3
    4
    set<string> country;
    country.insert("China"); //{"China"}
    country.insert("America"); //{"China","America"}
    //再次插入相同的元素不会被插入

  • 删除元素 时间复杂度o(logn)

    1
    2
    country.erase("America");	//{"China"}
    //删除不存在的元素不会报错，不会执行任何操作

  • 判断元素是否存在 时间复杂度o(logn)

    1
    2
    country.count("China");
    //若存在返回1，否则返回0

  • 使用迭代器访问元素

    1
    2
    3
    4
    for(set<string>::iterator it = country.begin(); it!=country.end(); it++){
        cout << *it <<endl;
    }
    //C++中遍历set是从小到大遍历，即排序好了

  • 获取元素个数 o(1)

    1
    country.size();

  • 清空 o(n)

    1
    country.clear();

  • 用set存储结构体，需要重载运算符 <

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    struct Node{
        int x, y;	//若x一致，比较y
        bool operator<(const Node &rhs) const{
            if(x == a.x){
                return y < rhs.y;
            }else{
                return x < rhs.x;
            }
        }
    };

    set保存结构体并输出-参考代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    #include <iostream>
    #include <set>
    using namespace std;
    struct Point{
        int x, y;
        bool operator <(const Point &rhs) const {
            if(x == rhs.x){
                return y < rhs.y;
            }else{
                return x < rhs.x;
            }
        }
    };


    int main(){
        int n=2;
        set<Point> p;
        //插入结构体
        for(int i=0; i<n; i++){
            Point temp;
            cin >> temp.x >> temp.y;
            p.insert(temp);
        }
        //输出结构体
        for(set<Point>::iterator it = p.begin(); it != p.end(); it++){
            cout << it -> x << " " << it -> y<<endl;
        }

    }

集合-map

结构为key-value，且key唯一

1
2
#include <map>
using namespace std;

  • 构造一个映射

    1
    2
    map<T1,T2> m;
    //这样就定义了一个名为m的从T1到T2类型映射

  • 插入映射 o(logn)

    1
    2
    3
    map<string, int> dict;
    dict.insert(make_pair("Banana",1));
    //若key已存在，不会插入新的value

  • 访问映射

    1
    2
    3
    dict["Banana"];		//这样可以获得1
    //若访问一个不存在的key，会自动生成映射，value默认值为0或空字符串（取决于value类型）
    dict["Banana"] = 2; 	//更改value

  • 判断key是否存在 o(logn)

    1
    2
    dict.count("Banana");
    //存在返回1，否则返回0

  • 迭代器访问map

    1
    2
    3
    4
    for(map<string,int>::iterator it = dict.begin(); it != dict.end(); it++){
        cout << it->first << "->" << it->second <<endl;	//first是key，second是value
    }
    //按照key从小到大遍历

  • 清空map o(n)

    1
    dict.clear();

    参考代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    #include <iostream>
    #include <map>
    using namespace std;
    int main(){
        map <string, int> dict;	//声明map
        dict["Tom"] = 1;				//访问并赋值
        dict["Mary"] = 2;
        dict["Hlo"] = 3;

        if(dict.count("Mary")){
            cout << "Mary id is" << dict["Mary"] << endl;
            dict["Mary"] = 10;
        }

        for(map<string,int>::iterator it = dict.begin(); it != dict.end(); it++){
            cout << it->first << "->" << it->second << endl;
        }

        dict.clear();
        return 0;
    }

    //输出结果(可以看到是排序后输出)：
    Mary id is2
    Hlo->3
    Mary->10
    Tom->1

综合例题

例1-打印锯齿矩阵

锯齿矩阵是指每一行包含的元素个数不相同的矩阵，例如

1
2
3
3 5 2 6 1
2 3 4
1 6 2 7

现读入若干整数(x,y)表示在第x行的末尾上加上一个元素y。输出最终的锯齿数组，初始时矩阵为空。

输入格式

第一行输入两个整数n,m(1≤n, m≤10000)，其中n表示锯齿数组行数，m表示插入元素总数。

接下来一共m行，每行两个整数x,y(1≤x≤n，0≤y≤10000)，表示在第x行的末尾插入一个元素y。

1
2
3
4
5
6
7
8
9
10
11
12
13
3 12
1 3
2 2
2 3
2 4
3 1
3 6
1 5
1 2
1 6
3 2
3 7
1 1

输出格式

一共输出n行，每行若干个用空格分隔的整数。如果某行没有任何元素，输出一个空行。

1
2
3
3 5 2 6 1
2 3 4
1 6 2 7

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
#include <vector>
using namespace std;
vector<int> mat[10005];	//定义vector
int main(){
    int n, m, x, y;
    cin >> n >> m;
    for(int i=0;i<m;i++){
        cin >> x >> y;
        mat[x].push_back(y);
    }
    for(int i=1; i<=n ;i++){
        for(int j=0; j< mat[i].size(); j++){
            if(j!=mat[i].size()-1){
                cout << mat[i][j] << " ";
            }else{
                cout << mat[i][j] << endl;
            }
        }
        cout << endl;   //注意空行
    }
    return 0;
}
/*此题考查动态数组的定义，用vector会使这种题变得很简单*/

例2-福尔摩斯破案

最近某地连续发生了多起盗窃案件，根据监控和路人提供的线索得知，这是-一个犯罪团伙。并且还知道这个犯罪团伙中每个人的身高、体重、年龄。警察想知道这个犯罪团伙中的每个人是不是本市的(如果本市有这个特征的人就视为是本市的)。但本市人口太多，又不能一个一个排查。警察又急需来帮忙解决这个棘手的问题。

输入格式
第一行将会输入两个数字n (1≤n≤2*10^5) 和 m (1≤m≤10^4)。 n代表本市的人口数目，m代表犯罪团伙的数量。
后面n行每行有3个数字代表本市每个人的身高、体重、年龄。然后会有m行每行有3个数字，代表犯罪团伙每个人的身高、体重、年龄。

1
2
3
4
5
6
3 2
166 50 30
178 60 23
132 40 15
167 50 30
178 60 23

输出格式

输出m行，每行输出一个"yes"或"no"，分别代表罪犯是本市的和不是本市的。

1
2
no
yes

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <set>
using namespace std;
struct people{
    int h;
    int w;
    int age;
    people(int _h, int _w, int _age){		//重写一个构造函数，方便后面传值
        h = _h;
        w = _w;
        age = _age;
    }
    bool operator<(const people &rhs) const{    //用set之前随意重写排序方法
        if(h!=rhs.h){
            return h < rhs.h;
        }
        if(w!=rhs.w){
            return w < rhs.w;
        }
        return age < rhs.age;
    }
};
set<people> s;
int main(){
    int n,m,h,w,age;
    cin >> n >> m;
    for(int i=0; i<n; i++){
        cin >> h >> w >> age;
        s.insert(people(h,w,age));
    }
    for(int i=0;i<m;i++){
        cin >> h >> w >> age;
        if(s.count(people(h,w,age))){
            cout << "yes" << endl;
        }else{
            cout << "no" << endl;
        }
    }
}
/*此题考查set集合与运算符重载，若不重载运算符存结构体时set无法排序会报错*/

例3-藏书计算

小明有个学霸同学，家中藏书真可谓汗牛充栋。小明想考一考学霸，给学霸出了-道难题。小明问这么多书籍，到底有多少本不一样的书，每样书的名字是什么? (因为有的书名是一样的，所以我们把它们视为同样的书) 学霸就是学霸，张口就说出了答案。不知道你是否也是学霸? 一起来挑战下?

输入格式

第一行是书籍总量 n(1≤n≤10^6)

然后有n行书名(书名是一个英文字符串，字符串的长度小于100，中间没有空格)。

1
2
3
4
5
4
English
Math
Chinese
Chinese

输出格式

第一行是不同书籍的数量

然后按照书名的字典序输出书名和数量。

1
2
3
4
3
Chinese 2
English 1
Math 1

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
#include <map>
#include <string>
using namespace std;
map <string, int> book;
int main(){
    int n;
    string name;
    cin >> n;
    for(int i=0; i<n; i++){
        cin >> name;
        book[name]++;   //若key不存在默认生成value为0，然后++添加数量
    }
    cout << book.size() << endl;
    for(map<string, int>::iterator it = book.begin(); it!=book.end(); it++){
        cout << it->first << " " << it->second << endl;
    }
    return 0;
}

由于题目给的n在六次方内，一般大于五次方的话用cout和cin效率较低，容易超时，下面用scanf和printf再写一遍

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <cstdio>
#include <map>
#include <string>
using namespace std;
map <string, int> book;
char name[105];	//创建一个数组来读取书名
int main(){
    int n;
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        scanf("%s", name);
        book[name]++;   //若key不存在默认生成value为0，然后++添加数量
    }
    printf("%d\n", book.size());
    for(map<string, int>::iterator it = book.begin(); it!=book.end(); it++){
        printf("%s %d\n",(it->first).c_str(), it->second);	//注意c_str用法
    }
    return 0;
}
/*此题考查map集合的使用方法，并且要注意由于数据量过大的时间超限问题*/

例4-堆积木

小明有n块积木，编号分别为1到n，一开始，小明把第i块积木放在位置i。小明进行m次操作，每次操作小明都把位置b上的积木整体移动到位置a上面。比如1位置的积木是1，2位置的积木是2，那么把位置2的积木移动到位置1后，位置1上的积木从下到上依次为1，2。

输入格式

第一行输入两个整数n, m(1≤n≤10000，0≤m≤10000)

接下来m行，每行输入两个整数a，b(1≤a, b≤n)，如果a，b相等则本次不需要移动

1
2
3
4
5
4 4
3 1
4 3
2 4
2 2

输出格式

输出n行，第i行输出位置i从下到上的积木编号

1
2
3
4

2 4 3 1


参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <cstdio>
#include <vector>
using namespace std;
vector<int> v[10005];
int main(){
    int n, m, a, b;
    scanf("%d%d", &n, &m);
    for(int i=1; i<=n; i++){
        v[i].push_back(i);
    }
    for(int i=0; i<m; i++) {
        scanf("%d%d", &a, &b);
        if (a == b) {
            continue;
        }
        for (int j = 0; j < v[b].size(); j++) {
            v[a].push_back(v[b][j]);
        }
        vector<int>().swap(v[b]);  //清空内存，防止爆栈
    }

    for(int i=1; i<=n; i++){
        for(int j=0; j<v[i].size(); j++){
            if(j!=v[i].size()-1){
                printf("%d ",v[i][j]);
            }else{
                printf("%d",v[i][j]);
            }
        }
        printf("\n");   //注意换行要放这里，若行为空也一样会输出空行
    }
    return 0;
}

例5-计算集合的并

给你两个集合，计算其并集，即{A}+{B}

输入格式

第一行输入两个数字n, m(0<n, m≤10000)，分别表示集合A和集合B的元素个数

后两行分别表示集合A和集合B的元素(int)，每个元素之间用一个空格隔开

1
2
3
1 2
1
1 2

输出格式

输出一行元素，表示合并后的集合，要求从小到大输出，元素之间用一个空格隔开

1
1 2

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <cstdio>
#include <set>
using namespace std;
set<int> s;
int main(){
    int n, m, x, cnt=0;
    scanf("%d%d",&n,&m);
    for(int i=0; i<n+m; i++){
        scanf("%d", &x);
        s.insert(x);
    }
    for(set<int>::iterator it = s.begin(); it!=s.end(); it++){
        if(cnt!=s.size()-1){
            printf("%d ", *it);
            cnt++;
        }else{
            printf("%d\n", *it);
        }
    }
    return 0;
}
/*此题考查set集合与迭代器的使用，较简单*/

例6-小明学英语

小明快要考六级了，这几天他每天早上都起来背单词。小红喜欢时不时考一考小明：小红问小明一个单词，如果小明背过这个单词，他会把这个单词的意思告诉小红，否则会跟小红说还没背过。单词是由连续的大写或小写字母组成，但是不区分大小写。比如Love和love是同一个单词。

输入格式

首先输入一个n(1≤n≤10000)表示事件数。接下来n行每行表示一个事件。每个事件输入一个整数d和一个单词word（长度不大于20），用空格隔开。如果d=0，表示小明记住了这个单词，如果d=1，表示这是一个测试，测试小明是否认识这个单词（小红不会告诉小明单词是什么意思）。事件的输入是按照先后顺序输入的。

1
2
3
4
5
6
5
0 we
0 are
1 family
0 Family
1 Family

输出格式

对于小红的每次测试，如果小明认识这个单词输出Yes，否则输出一行No

1
2
No
Yes

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <set>
#include <string>
using namespace std;
string word;
set<string> s;
int main(){
    int n, d;
    cin >> n;
    for(int i=0; i<n; i++){
        cin >> d >> word;
        for(int j=0; j< word.size(); j++){  //将大写字母转换为小写字母
            if(word[j]>='A' && word[j]<= 'Z'){
                word[j] -= 65;
            }
        }
        if(d == 0){
            s.insert(word);
        }else{
            if(s.count(word)){
                cout << "Yes\n" << endl;
            }else{
                cout << "No\n" << endl;
            }
        }
    }
}
/*此题考查set集合的应用，注意先排除大写字母的干扰*/

例7-小明转专业（转专业真题）

小明在转学校计算机专业时，曾在上机考试遇到过这样一个题：

给定n个整数，求里面出现次数最多的数，如果有多个重复出现的数，求出值最大的一个。当时可是把小明难住了，现在请你来解决一下。

注：此题为天津理工大学2018级转计算机专业c语言上机题1

输入格式

第一行输入一个整数n(1≤n≤100000)，接下来一行输入n个int范围的整数

1
2
5
1 1 2 3 4

输出格式

输出出现次数最多的数和出现的次数，用一个空格隔开。如果有多个重复出现次数一样的数，输出值最大的那个。

1
1 2

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <cstdio>
#include <map>
using namespace std;
map<int, int> mp;
int main(){
    int n, x, ans, time;   //ans存输出的数，time存出现的次数
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        scanf("%d", &x);
        mp[x]++;    //若key不存在，value默认值为0，再+1
    }
    time = 0;
    for(map<int, int>::iterator it = mp.begin(); it!=mp.end(); it++){
        if( (it->second)>= time ){	//比较出现次数，若次数更多则赋值
            time = (it->second);
            ans = (it->first);
        }
    }
    printf("%d %d\n", ans, time);
}
/*此题考查map的综合应用。在转专业考试时，小明的思路是开拓一个大于输入个数n的数组，将出现的数次数存在该数对应下标位置的数组中。
此方法有很大的缺点：浪费了大量空间，最后还要遍历一遍数组找次数相等但值最大的元素。如果运用stl中的map集合，这种题会变得非常简单。*/

例8-水果店

小明经营着一个不大的水果店。他认为生存之道是经营最受顾客欢迎的水果。现在他想要一份水果销售状况的明细表，这样就可以很容易掌握所有水果的销售情况。小明告诉你每一笔销售记录的水果名称，产地和销量，请你帮他生成明细表。

输入格式

第一行是一个整数N(0<N≤1000)，表示共有N次成功的交易。随后有N行数据，每行表示一次交易，由水果名称（小写字母，长度不超过100）和交易的产地（小写字母，长度不超过100）水果数目（正整数，不超过长度1000）组成。

1
2
3
4
5
6
5
apple shandong 3
pineapple guangdong 1
sugarcane guangdong 1
pineapple guangdong 3
pineapple guangdong 1

输出格式

请你输出一份排版格式正确（请分析样本输出）的水果销售明细表。这份表包括所有水果的名称、产地和销量。水果先按产地分类，产地按字母顺序排序。同一产地的水果按照名称排序，名称按字母顺序排序。

1
2
3
4
5
guangdong
    |----pineapple(5)
    |----sugarcane(1)
shandong
    |----apple(3)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
#include <map>
using namespace std;
map<string, map<string, int>> mp;
string s1,s2;
int d;
int main(){
    int n;
    cin >> n;
    for(int i=0; i<n; i++){
        cin >> s1 >> s2 >> d;
        mp[s2][s1] += d;
    }
    for(map<string,map<string, int>>::iterator it1 = mp.begin(); it1 != mp.end(); it1++){
        cout << (it1->first) << endl;
        for(map<string, int>::iterator it2 = (it1->second).begin(); it2!=(it1->second).end(); it2++){
            cout << "    |----" << (it2->first) << "(" << (it2->second) <<")" << endl;
        }
    }
    return 0;
}
/*此题考查map的高级应用：在map中再嵌套一个map，重点是要学会存入和读取map中的map。*/

七.栈与递归

栈

  • 栈是一种特殊的线性结构，有后进先出的特性，只能在一端进行操作

    参考入栈、出栈、取栈顶元素代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    #include <iostream>
    using namespace std;
    struct Stack{
        int data[10000];
        int top = -1;
        //进栈
        void push(int x){
            top++;
            if(top<10000){
                data[top]=x;
            } else{
                top--;
                cout<<"Stack overflow!"<<endl;
            }
        }
        //出栈
        void pop(){
            if(top>=0){
                top--;
            }
        }
        //求栈顶元素
        int topval(){
            if(top>=0){
                return data[top];
            }
            return 0;
        }
    };
    int main(){
        Stack s;
        for(int i=1; i<=10; i++){
            s.push(i);
        }
        for(int i=1;i<=10;i++){
            cout<<s.topval()<<" ";
            s.pop();
        }
        return 0;
    }

  • 在C++标准库中，提供了stack，功能齐全且易于使用，如stack <T> s代表定义了一个存储T类型的栈s。你可以对他进行push\pop\top\empty\size等函数的调用

    方法 功能 参数类型 返回值类型
    push 压入元素到栈顶 T
    pop 弹出栈顶元素
    top 返回栈顶元素
    empty 判断栈是否为空 bool
    size 栈的元素个数 非负整数

递归

  • 递归是编程中应用广泛的一个技巧，就是函数调用函数自身

  • 递归例子-汉诺塔（可自行百度问题）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    #include <iostream>
    #include <stack>
    using namespace std;
    stack<int> S[3];    //三个柱子
    void move(int x, int y){
        int temp = S[x].top();
        S[x].pop();
        S[y].push(temp);
        cout << x << "-->" << y << endl;
    }
    //A为圆盘一开始所在柱子， B为中间柱子， C代表目标柱，n代表移动盘子个数
    void hanoi(int A, int B, int C, int n){
        //递归终止条件
        if(n == 1){
            move(A, C); //从A柱子直接移动到C柱子
            return;
        }
        hanoi(A,C,B,n-1);
        move(A,C);
        hanoi(B,A,C,n-1);

    }
    int main(){
        int n;
        cin >> n;
        for(int i=n; i>=1; i--){    //大盘子先进栈
            S[0].push(i);
        }
        hanoi(0,1,2,n);
        while(!S[2].empty()){
            cout << S[2].top() << " ";
            S[2].pop();
        }
        return 0;
    }

综合例题

例1-小明吃桃

小明买了一堆桃子不知道个数，第一天吃了一半的桃子，还不过瘾，又吃多了一个。以后他每天吃剩下的桃子的一半还多一个，到n天只剩下一个桃子了。小明想知道一开始买了多少桃子。

输入格式

输入一个整数n(2≤n≤30)

1
2

输出格式

输出买的桃子的数量

1
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <cstdio>
int n;
int f(int x){
    if(x == n){ //到第n天只剩下一个桃子
        return 1;
    }else{
        return (f(x+1)+1)*2;
    }
}
int main(){
    scanf("%d", &n);
    printf("%d\n",f(1));
    return 0;
}
/*此题考查递归，注意终止条件*/

例2-修改后的斐波那契数列

相信很多人都学过斐波那契数列，它是：1,1,2,3,5,8,13,21…这样一个数列

用fn表示斐波那契数列的第n项，则有：f1=f2=1, fn=fn-1+fn-2(n＞2)

为了提高难度，现修改了公式，新的公式：f1=f2=1, fn=afn-1+fn-2 (n＞2)

输入格式

输入每行包括四个整数 n(1≤n≤100) ，a(1≤a≤10)，b(1≤b≤10)，p(1≤p≤2000)

1
3 1 1 1000

输出格式

输出fn对p取模的值

1
2

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <cstdio>
int ans[2005];
bool vis[2005];
int f(int n, int a, int b, int p){
    if(vis[n]){
        return ans[n];
    }
    vis[n] = true;
    if(n == 1||n == 2){
        return ans[n] = 1%p;
    }else{
        return ans[n] = (a*f(n-1, a, b, p) % p + b*f(n-2,a,b,p) % p)%p;
    }
}
int main(){
    int n, a, b, p;
    scanf("%d%d%d%d", &n,&a,&b,&p);
    printf("%d\n",f(n,a,b,p));
    return 0;
}

例3-快速幂

x^y相信大家都会计算（for循环相乘），但y很大时怎么办？

小明研究发现，找到了一个好办法，公式如下

1
2
3
f(x,y) = f(x,y/2)*f(x,y/2) ----------- y%2==0 && y>0
f(x,y) =1 ------------------------------ y=0
f(x,y) = f(x,y/2)*f(x,y/2) *x -------- y%2==1 && y>0

（当然这不是快速幂的最好写法）

输入格式

第一行输入整数t(t≤100)

随后t行，每行三个整数x(1≤x≤10^9)，y(1≤y≤10^18)，p(1≤p≤10^9)

1
2
1
2 10 10000

输出格式

输出x^y%p的值

1
1024

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <cstdio>
long long f(long long x, long long y, long long p){
    if (y == 0){
        return 1%p;
    }else if (y % 2==0){
        long long temp = f(x, y/2, p);
        return temp*temp % p;   //注意要用temp保存下来，否则递归两次浪费时间
    }else{
        long long temp = f(x, y/2, p);
        return temp*temp % p * x % p;
    }
}
int main(){
    int t;
    long long x,y,p;
    scanf("%d",&t);
    while(t--){
        scanf("%lld%lld%lld", &x, &y, &p);
        printf("%lld\n", f(x,y,p));
    }
    return 0;
}
/*此题考查递归，注意由于元素过大要用long long类型保存，不能完全计算出来再取模，容易超空间*/

例4-弹簧板

有一个小球落在一串连续的弹簧板上，小球落到某一个弹簧板后，会被弹到某一个地点，直到小球被弹到弹簧板以外的地方。

假设有n个连续的弹簧板，每个弹簧板占一个单位举例。第i个弹簧板能选择把小球向前弹a[i]个距离，或者向前弹b[i]个距离。比如位置1的弹簧能让小球前进2个距离到达位置3。

现在小球掉到了1弹簧板上面，请你帮忙计算小球最少会被弹起多少次，才会弹出弹簧板。1号弹簧板也算一次。

输入格式

第一行输入一个n代表有n个弹簧板(1≤n≤200)

第二行输入n个数字，中间用空格隔开。第i个数a[i]（0<a[i]<30）代表第i个弹簧板可以让小球移动的距离。

第二行输入n个数字，中间用空格隔开。第i个数b[i]（0<b[i]<30）代表第i个弹簧板可以让小球移动的距离。

1
2
3
5
2 2 3 1 2
1 2 3 4 1

输出格式

输出一个整数，表示小球被弹起的最小次数

1
2

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <cstdio>
#include <algorithm>
using namespace std;
int a[205],b[205];
int ans[205];
bool vis[205];
int n;
int f(int x){   //传入一次前进距离，返回弹起次数
    if(x >= n){
        return 0;
    }
    if(vis[x]){
        return ans[x];
    }
    vis[x] = true;
    return ans[x] = min(f(x+a[x]), f(x+b[x])) + 1;
}
int main(){
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        scanf("%d", &a[i]);
    }
    for(int i=0; i<n; i++){
        scanf("%d", &b[i]);
    }
    printf("%d\n",f(0));
}
/*此题考查递归条件的判断，有一定难度*/

例5-最大公约数

最大公约数相信大家都会计算，但怎么用计算机快速的计算呢？

f(x,y) = f(y, x%y), y>0

f(x,y) = x , x=0

输入格式

第一行输入一个整数t (t≤100)

然后有t行，每行有两个整数x(1≤x≤10^9)，y(1≤y≤10^9)

1
2
1
6 8

输出格式

输出x，y的最大公约数

1
2

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <cstdio>
int gcd(int x, int y){
    if(y == 0){
        return x;
    } else{
        return gcd(y, x%y);
    }
}
int main(){
    int t,x,y;
    scanf("%d", &t);
    while (t--){
        scanf("%d%d", &x, &y);
        printf("%d", gcd(x,y));
    }
    return 0;
}

例6-括号匹配

小明在纸上写了一个字符串，只包含’(‘和’)’ 。一个’(‘能匹配一个’)‘，但是匹配的’(‘必须出现在’)'之前。请你帮小明判断下他写的字符串能否完全匹配，如果能则输出括号的位置。（匹配的括号不能交叉，只能嵌套）

输入格式

一行输入一个字符串只含有’(‘和’)’ ，输入的字符串长度不大于50000

1
(())

输出格式

如果输出的括号不匹配，输出一行"No"，否则输出一行"Yes"，接下来里若干行每行输出两个整数，用空格隔开，表示所有匹配对的括号的位置（下标从1开始）。可以按任意顺序输出。

1
2
3
Yes
2 3
1 4

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <cstdio>
#include <cstring>
#include <stack>
using namespace std;
stack<int> st;
char s[50005];
int ans[50005];
int main(){
    scanf("%s", &s);
    int len = strlen(s);
    bool b = true;
    for(int i=0;i<len;i++){
        if(s[i]=='('){
            st.push(i+1);   //注意题目要求下标从1开始
        }else{
            if(!st.empty()){
                ans[i+1]=st.top();	//获取栈顶元素（位置）
                st.pop();
            } else{     //右括号多余
                b=false;
                break;
            }
        }
    }
    if(!st.empty()){    //左括号多余
        b=false;
    }
    if(!b){
        printf("No\n");
    }else{
        printf("Yes\n");
        for(int i=1; i<=len; i++){
            if(ans[i]){
                printf("%d %d\n",ans[i],i);
            }
        }
    }

    return 0;
}
/*括号匹配类似的题都可以使用栈进行操作，本题答案不唯一，只要输出全部匹配的位置就行*/

例7-网页跳转

小明每天都在使用一款名为"515code游览器"的软件，软件一共有三种操作：打开页面、前进、后退。它们的功能如下所示：

  • 打开页面：在地址栏中输入网址，并跳转到相应页面
  • 后退：返回到上一次游览的界面
  • 前进：返回到上次后退前的界面，如果上一次操作是打开界面，则无法前进

现在，小明打开了这个软件，进行了一系列操作，你需要输出他每次操作后所在页面的地址。

输入格式

第一行输入一个整数n(0＜n≤100000)，表示小明的操作次数

接下来n行，每行输入一个字符串，如果是VISIT，后面接着输入一个不含有空格和换行的网址（长度小于100），表示小明在游览器中输入的网址；如果是BACK，表示小明点击了后退按钮；如果是FORWARD，表示小明点击了前进按钮。

1
2
3
4
5
6
7
8
9
10
11
10
VISIT https://www.baidu.com/
VISIT https://www.515code.com/
BACK
BACK
FORWARD
FORWARD
BACK
VISIT https://www.google.com/
FORWARD
BACK

输出格式

对于每次操作，如果小明操作成功，输出小明操作后的网址，否则输出Ignore。假设小明输入的网址都是合法的。

1
2
3
4
5
6
7
8
9
10
11
https://www.baidu.com/
https://www.515code.com/
https://www.baidu.com/
Ignore
https://www.515code.com/
Ignore
https://www.baidu.com/
https://www.google.com/
Ignore
https://www.baidu.com/
Process finished with exit code 0

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <stack>
#include <string>
using namespace std;
string op, s;
stack<string> s1, s2;   //s2记录被s1弹出的记录
int main(){
    int n;
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        cin >> op;
        if(op == "VISIT"){
            cin >> s;
            while(!s2.empty()){
                s2.pop();
            }
            s1.push(s);     //访问网站时，网址压入s1栈中
        }else if(op == "BACK"){
            if(s1.size()<=1){   //无法后退
                cout << "Ignore" <<endl;
                continue;
            }
            s2.push(s1.top());  //s1出栈的记录保存在s2中
            s1.pop();
        }else{
            if(s2.empty()){     //无法前进
                cout << "Ignore" <<endl;
                continue;
            }
            s1.push(s2.top());  //s2出栈的记录保存在s1中
            s2.pop();
        }
        cout << s1.top()<< endl;
    }
    return 0;
}

/*此题考查栈的设计应用，注意判断两个栈的出栈和入栈条件，容易出错！*/

八.深度优先搜索

  • 深度优先搜索（dfs）是一种算法，注重的是思想，把所有可行的方案都列出来不断的去尝试，直到找到问题的解

  • 经典：迷宫问题

    给定任意一个迷宫地图，求解路径

    输入样例

    1
    2
    3
    4
    5
    6
    5 6
    ....S*
    .***..
    .*....
    *.**..
    .E....

    输出样例

    1
    2
    3
    4
    5
    ....+*
    .***+.
    .*..+.
    *.**+.
    .E+++.

    参考代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    #include <iostream>
    #include <string>
    using namespace std;
    int n, m;
    string maze[110];
    bool vis[110][110];
    int dir[4][2]={{-1,0},{0,-1},{1,0},{0,1}};   //左下右上四个方向
    bool in(int x, int y){
        return 0<=x && x<n && 0<=y && y<m;
    }
    bool dfs(int x, int y){
        if(maze[x][y] == 'E'){
            return true;
        }
        vis[x][y]=1;    //表示此坐标已经访问过
        maze[x][y] ='+';    //标记通路

        for(int i=0; i<4; i++){
            int tx = x + dir[i][0];
            int ty = y + dir[i][1];
            if(in(tx, ty) && maze[tx][ty]!='*' && !vis[tx][ty]){
                if(dfs(tx, ty)){
                    return true;
                }
            }
        }

        vis[x][y]=0;
        maze[x][y]='.';
        return false;

    }

    int main(){
        //输入迷宫地图，'.'代表通路，'*'代表墙壁，'S'代表起点，'E'代表终点
        cin >> n >> m;
        for(int i=0; i<n; i++){
            cin >> maze[i];
        }
        int x, y;
        for(int i=0; i<n; i++){
            for(int j=0; j<m; j++){
                if(maze[i][j] == 'S'){
                    x = i, y = j;
                }
            }
        }
        if(dfs(x,y)){
            for(int i=0; i<n; i++){
                cout << maze[i] << endl;
            }
        } else{
            cout << "走不通" << endl;
        }
    }

例题1-中国象棋

中国象棋博大精深，其中马的规则最为复杂，也是最难操控的一颗棋子。

我们都知道象棋中马走"日"，比如在 (2, 4)位置的一个马，跳一步能到达的位置有 (0, 3)，(0, 5)，(1, 2)，(1, 6)，(3, 2)，(3, 6)，(4, 3)，(4, 5)

中国象棋题目

小明正在和小红下棋，小明正在进行战略布局，他需要把在 (x,y)位置的马跳到 (x’, y’) 位置，以达到威慑的目的。

但是棋盘大小有限制，棋盘是一个 10*9 的网格，左上角坐标为 (0, 0)，右下角坐标为 (9, 8)，马不能走出棋盘，并且有些地方已经有了棋子，马也不能跳到有棋子的点。

蒜头君想知道，在不移动其他棋子的情况下，能否完成他的战略目标。

输入格式

一共十行，每行一个长度为9的字符串

输入表示这个棋盘，用’.‘表示空位置，用’#'表示该位置有棋子，用’S’表示马的初始位置，用’T’表示马需要跳到的位置。

输入保证一定只存在一个’S’和一个’T’。

1
2
3
4
5
6
7
8
9
10
.#....#S#
..#.#.#..
..##.#..#
......##.
...T.....
...#.#...
...#.....
...###...
.........
.##......

输出格式

如果在不移动其他棋子的情况下，马能从’S’跳到’T’，那么输出一行"Yes"，否则输出一行"No"

1
Yes

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <cstdio>
char s[10][10];
//定义八个方向，分别为上图所示的点
int dir[8][2] = {{2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}};
bool vis[10][10];   //记录是否访问过
bool f = false;
bool in(int x, int y){
    return 0<=x && x<10 && 0<=y && y<9;
}
void dfs(int x, int y){
    vis[x][y] = true;
    if(f){
        return;
    }
    if(s[x][y]=='T'){
        f = true;
    }
    for(int i=0; i<8; i++){
        int tx = x + dir[i][0];
        int ty = y + dir[i][1];
        if(in(tx, ty) && s[tx][ty] != '#' && !vis[tx][ty]){
            dfs(tx, ty);
        }
    }
}
int main(){
    int x, y;
    for(int i=0; i<10; i++){
        scanf("%s", &s[i]);
    }
    for(int i=0; i<10; i++){
        for(int j=0; j<9; j++){
            if(s[i][j] == 'S'){	//找到马的位置
                x = i;
                y = j;
            }
        }
    }
    dfs(x, y);	//搜索
    if(f){
        printf("Yes\n");
    }else{
        printf("No\n");
    }
    return 0;
}
/*此题考查dfs，注意返回条件与边界条件的判断，容易出错*/

例题2-踏青

小明和他的朋友周末相约去召唤师峡谷踏青。他们发现召唤师峡谷的地图是由一块一块格子组成，有的格子上是草丛，有的是空地。草丛通过上下左右4个方向拓展其他草丛形成一片草地，任何一片草地中的格子都是草丛，并且所有格子之间都能通过上下左右联通。如果用’#‘代表草地，’.'代表空地，下面的峡谷则有2片草地

1
2
##..
..##

处在同一片草地的2个人可以互相看到，空地看不到草地里面的人。他们发现有一个朋友不见了，现在需要分头去找，每个人负责一片草地，小明想知道他们至少需要多少人

输入格式

第一行输入n,m(1≤n , m≤100)表示峡谷大小

接下来n行字符串表示峡谷的地形

1
2
3
4
5
6
5 6
.#....
..#...
..#..#
...##.
.#....

输出格式

1
5

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <cstdio>
char mp[105][105];
bool vis[105][105];
int n, m;
void dfs(int x, int y){
    //判断边界和特殊情况
    if(x<0 || x>=n || y<0 || y>=m || vis[x][y] || mp[x][y]=='.'){
         return;
    }
    vis[x][y] = true;
    dfs(x-1, y);
    dfs(x+1, y);
    dfs(x,y-1);
    dfs(x,y+1);
}
int main(){
    int cnt=0;
    scanf("%d%d",&n,&m);
    for(int i=0; i<n; i++){
        scanf("%s",mp[i]);
    }
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            if(!vis[i][j] && mp[i][j] =='#'){
                dfs(i, j);  //搜索
                cnt++;
            }
        }
    }
    printf("%d\n",cnt);
}
/*本题其实就是求有多少片草地，利用深搜标记连续的草地（即一片草丛），注意边界条件判断*/

例题3-迷宫问题的方案数

给出一个迷宫，求其路径的方案数目

输入格式

第一行输入两个整数n(1≤n≤11)，m(1≤m≤11)表示迷宫的行和列

然后有一个n*m的地图，地图由四部分组成，'.‘表示可以通行的路，’#'表示迷宫的墙，'s’表示起点，'e’表示终点

1
2
3
4
5
6
5 5
s####
..###
..###
..###
....e

输出格式

输出一个整数，表示’s’到’e’的所有方案数

1
1

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<cstdio>
int n,m,x,y,ans;    //x,y为起始点坐标
char mp[15][15];
bool vis[15][15];
void dfs(int x, int y){
    if(x<0 || x>=n || y<0 || y>=m || vis[x][y] || mp[x][y]=='#'){
        return;
    }
    if(mp[x][y] == 'e'){
        ans++;
        return;
    }
    vis[x][y] = true;   //标记已访问过
    dfs(x-1,y);
    dfs(x+1,y);
    dfs(x,y-1);
    dfs(x,y+1);
    vis[x][y] = false;  //取消标记，因为要计算多条路径
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++){
        scanf("%s",&mp[i]);
    }
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(mp[i][j]=='s'){
                x=i;
                y=j;
            }
        }
    }
    dfs(x,y);
    printf("%d\n",ans);
    return 0;
}

正在持续更新，4月13日已更新